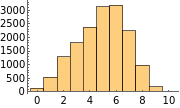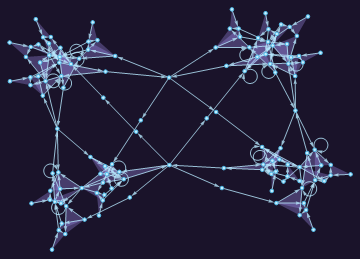
Universe 11114 from The Wolfram Physics Project

5 steps

wm11114`wm11114`

signature

1₂2₃→4₂4₃

rule

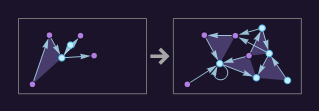
{{{1, 2, 3}, {4, 3, 5}, {3, 6}} -> {{6, 7, 8}, {6, 9, 10}, {11, 8, 10}, {5, 2, 9}, {9, 9}, {1, 9}, {7, 5}, {8, 5}}}

make editable copy
download notebook

Basic Evolution

Basic evolution:

[◼]	WolframModel

[{{{1,2,3},{4,3,5},{3,6}}{{6,7,8},{6,9,10},{11,8,10},{5,2,9},{9,9},{1,9},{7,5},{8,5}}},{{1,1,1},{1,1,1},{1,1}},5,"StatesPlotsList"]





Event-by-event evolution:

[◼]	WolframModel

[{{{1,2,3},{4,3,5},{3,6}}{{6,7,8},{6,9,10},{11,8,10},{5,2,9},{9,9},{1,9},{7,5},{8,5}}},{{1,1,1},{1,1,1},{1,1}},<|"MaxEvents"6|>,"EventsStatesPlotsList"]





Vertex and edge counts:

{vertexCountList,edgeCountList}=

[◼]	WolframModel

[{{{1,2,3},{4,3,5},{3,6}}{{6,7,8},{6,9,10},{11,8,10},{5,2,9},{9,9},{1,9},{7,5},{8,5}}},{{1,1,1},{1,1,1},{1,1}},13,{"VertexCountList","EdgeCountList"}];

ListLogPlot{vertexCountList,edgeCountList},

SequenceIcon



	vertices
	edges

Symbolic expression for vertex count:

FindSequenceFunction[vertexCountList,t]

DifferenceRootFunction{y.,n.},-2-2y.[n.]+y.[1+n.]0,y.[1]1,y.[2]6[t]

Symbolic expression for edge count:

FindSequenceFunction[edgeCountList,t]

(-4+5

)

Result after

generations:

WolframModel[

]

["FinalStatePlot"]

Causal Graph

Causal graph:

WolframModel[

]

"CausalGraph",

Rule[

]



Layered rendering:

WolframModel[

]

["LayeredCausalGraph"]

Causal graph distance matrix:

MatrixPlotTransposeGraphDistanceMatrix

WolframModel[

]

["CausalGraph"],

ListIcon



Final State Properties

Hypergraph adjacency matrix:

MatrixPlotAdjacencyMatrix@CatenateMapUndirectedEdge@@@Subsets[#,{2}]&,

WolframModel[

]

["FinalState"],

ListIcon



Vertex degree distribution:

HistogramValuesCountsCatenateUnion/@

WolframModel[

]

["FinalState"],

ListIcon



Neighborhood volumes (ignoring directedness of connections):

volumes=

[◼]	RaggedMeanAround

Values

[◼]	HypergraphNeighborhoodVolumes



WolframModel[

]

["FinalState"],All,Automatic;

ListLogLogPlotvolumes,

ListIcon



Effective dimension versus radius:

ListLinePlot

[◼]	LogDifferences

[volumes],

ListIcon



Successive neighborhood balls around a random vertex:

[◼]	HypergraphNeighborhoods



WolframModel[

]

["FinalState"],4





Distance matrix:

distanceMatrix=GraphDistanceMatrixUndirectedGraph

[◼]	HypergraphToGraph



WolframModel[

]

["FinalState"];

MatrixPlotExp[-(distanceMatrix/.0None)],

ListIcon



Distribution of distances in the graph:

HistogramFlatten[distanceMatrix],

ListIcon



Spreading of Effects

Causal graph adjacency matrix:

MatrixPlotAdjacencyMatrix

WolframModel[

]

["CausalGraph"],

ListIcon



Neighborhood volumes in causal graph:

ListLogLogPlotValues

[◼]	GraphNeighborhoodVolumes



WolframModel[

]

["CausalGraph"],{1},

ListIcon



Other Evolution Orders

Random evolutions:

[◼]	WolframModel

[{{{1,2,3},{4,3,5},{3,6}}{{6,7,8},{6,9,10},{11,8,10},{5,2,9},{9,9},{1,9},{7,5},{8,5}}},{{1,1,1},{1,1,1},{1,1}},<|"MaxEvents"31|>,"FinalStatePlot","EventOrderingFunction""Random"]

Different deterministic evolution orders:

[◼]	WolframModel

[{{{1,2,3},{4,3,5},{3,6}}{{6,7,8},{6,9,10},{11,8,10},{5,2,9},{9,9},{1,9},{7,5},{8,5}}},{{1,1,1},{1,1,1},{1,1}},<|"MaxEvents"31|>,"EventOrderingFunction"{#,"LeastRecentEdge","RuleOrdering","RuleIndex"}]["FinalStatePlot",PlotLabel#]&/@{"OldestEdge","LeastOldEdge","LeastRecentEdge","NewestEdge","RuleOrdering","ReverseRuleOrdering"}

