Tools Created for This Project
A variety of new functions have been added to the Wolfram Function Repository to directly implement, visualize and analyze the models defined here [201].
Basic Direct Symbolic Transformation
The class of models defined here can be implemented very directly just using symbolic transformation rules of the kind on which the Wolfram Language [98] is based.
It is convenient to represent relations as Wolfram Language lists, such as {1,2}. One way to represent collections is to introduce a symbolic operator σ that is defined to be flat (associative) and orderless (commutative):
Thus we have, for example:
We can then write a rule such as
more explicitly as:
This rule can then be applied using standard Wolfram Language pattern matching:
The Module causes a globally unique new symbol to be created for the new node z every time it is used:
But in applying the rule to a collection with more than one relation, there is immediately an issue with the updating process. By default, the Wolfram Language performs only a single update in each collection:
As discussed in the main text, there are many possible updating orders one can use. A convenient way to get a whole “generation” of update events is to define an inert form of collection σ1 then repeatedly replace collections σ until a fixed point is reached:
By replacing σ1 with σ at the end, one gets the result for a complete generation update:
NestList applies this whole process repeatedly, here for 4 steps:

Replacing σ by a Graph operator, one can render the results as graphs:
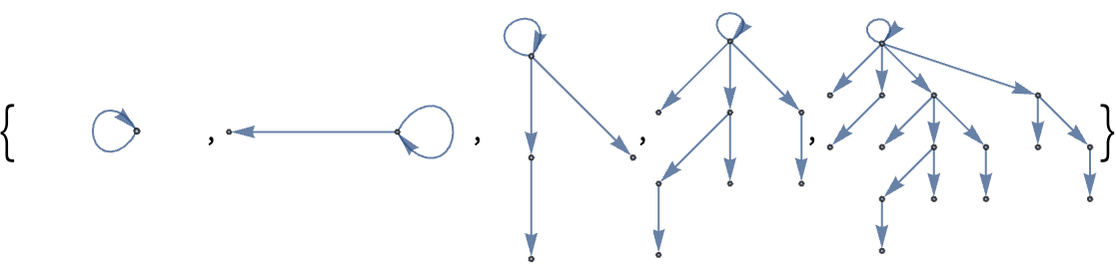
IndexGraph creates a graph in which nodes are renamed sequentially:
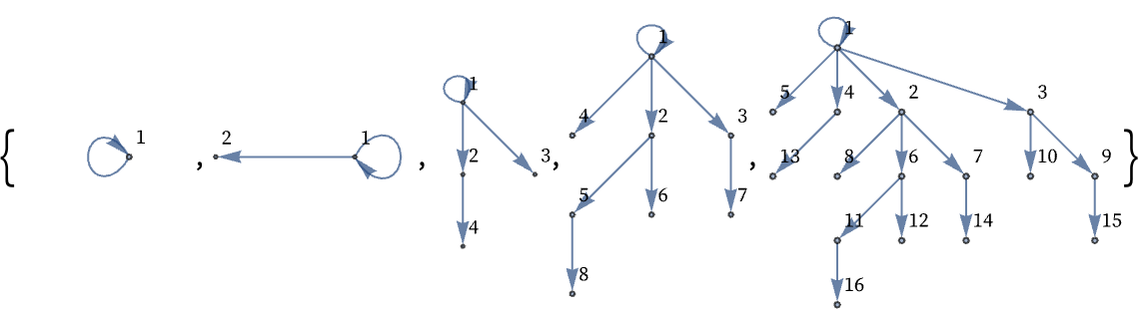
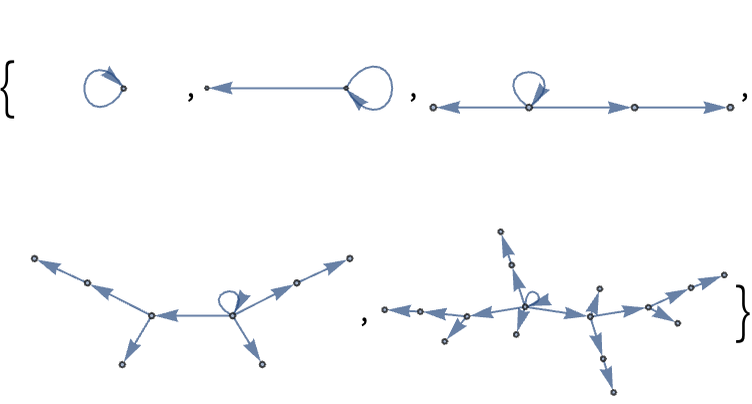
Here is the result with a different graph layout:
Exactly the same approach works for rules that involve multiple relations. For example, consider the rule:
This can be run for 2 steps using:

Here is the result after 10 steps, rendered as a graph:
Alternative Syntactic Representation
As an alternative to introducing an explicit head such as σ, one can use a system-defined matchfix operator such as AngleBracket (entered as <, >) that does not have a built-in meaning. With the definition
one immediately has for example
and one can set up rules such as
Pattern Sequences
Instead of having an explicit “collection operator” that is defined to be flat and orderless, one can just use lists to represent collections, but then apply rules that are defined using OrderlessPatternSequence:
Note that even though the pattern appears twice, /. applies the rule only once:
Subset Replacement
Yet another alternative is to use the function SubsetReplace (built into the Wolfram Language as of Version 12.1). SubsetReplace replaces subsets of elements in a list, regardless of where they occur:
Unlike ReplaceAll (/.) it keeps scanning for possible replacements even after it has done one:
One can find out what replacements SubsetReplace would perform using SubsetCases:
This uses SubsetReplace to apply a rule for one of our models; note that the rule is applied twice to this state (Splice is used to make the sequence of lists be spliced into the collection):
This gives the result of 10 applications of SubsetReplace:
This turns each list in the collection into a directed edge, and renders the result as a graph:
IndexGraph can then for example be used to relabel all elements in the graph to be sequential integers.
Note that SubsetReplace does not typically apply rules in exactly our “standard updating order”.
Parallelization
Our models do not intrinsically define updating order (see section 6), and thus allow for asynchronous implementation with immediate parallelization, subject only to the local partial ordering defined by the graph of causal relationships (or, equivalently, of data flows). However, as soon as a particular sequence of foliations—or a particular updating order—is defined, its implementation may require global coordination across the system.
 download pdf
download pdf  ARXIV
ARXIV peer review
peer review