Given any two points in a graph or hypergraph one can find a (not necessarily unique) shortest path (or “geodesic”) between them, as measured by the number of edges or hyperedges traversed to go from one point to the other. Here are a few examples of such geodesics:
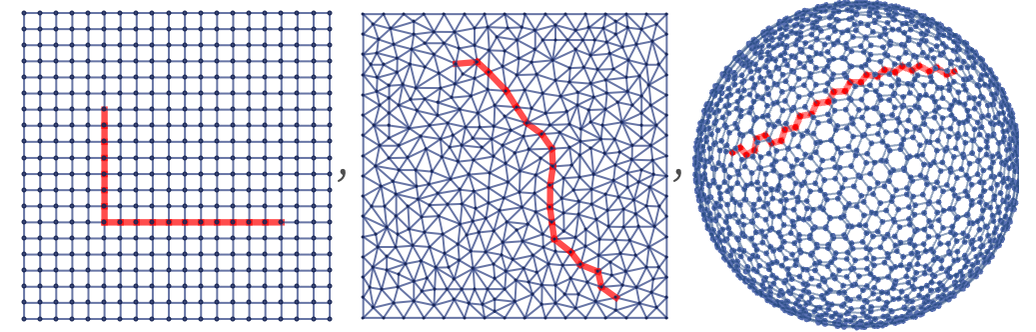
A geodesic in effect defines the analog of a straight line in a graph or hypergraph, and by analogy with the way geodesics work in continuous spaces, we can use them to probe emergent geometry.
For example, in the case of positive curvature, we can expect that nearby geodesics diverge, while in the case of negative curvature they converge:

One can see the same effect in sufficiently large graphs (although it can be obscured by regularities in graphs which lead to large numbers of “degenerate” geodesics, all of the same length):
We saw before that the growth rate of the volume Vr(X) of a ball centered at some point X in a graph could be identified as giving a measure of the Ricci scalar curvature R at X. But we can now consider tubes formed from balls centered at each point on a geodesic. And from the growth rates of volumes of these tubes we will be able to measure what can be identified as different components of curvature associated with the Ricci tensor (cf. [1:p1048][27][42]).
In a continuous space (or, more precisely, on a Riemannian manifold) the infinitesimal volume element at a point X is given in terms of the metric tensor g by ![]() . If we look at a nearby point X + δx we can expand in a power series in δx (e.g. [43])
. If we look at a nearby point X + δx we can expand in a power series in δx (e.g. [43])
where Rij is the Ricci tensor and the δi (contravariant vectors) are orthogonal components of δx (say along axes defined by some coordinate system).
If we integrate over a ball of radius r in d dimensions, we recover our previous formula for the volume of a ball
where R = ∑Rii is the Ricci scalar curvature.
But now let us consider integrating over a tube of radius r that goes a distance δ along a geodesic starting at X. Then we get a formula for the volume of the tube (cf. [44])
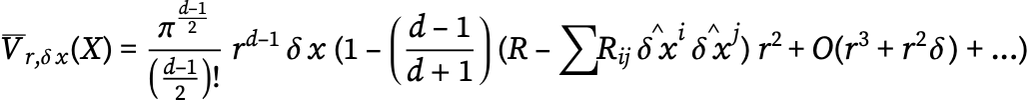
where the ![]() are components of unit vectors along the geodesic.
are components of unit vectors along the geodesic.
There is now a direct analog in our hypergraphs: just as we measured the growth rates of geodesic balls to find Ricci scalar curvature, we can now measure growth rates of geodesic tubes to probe full Ricci curvature.
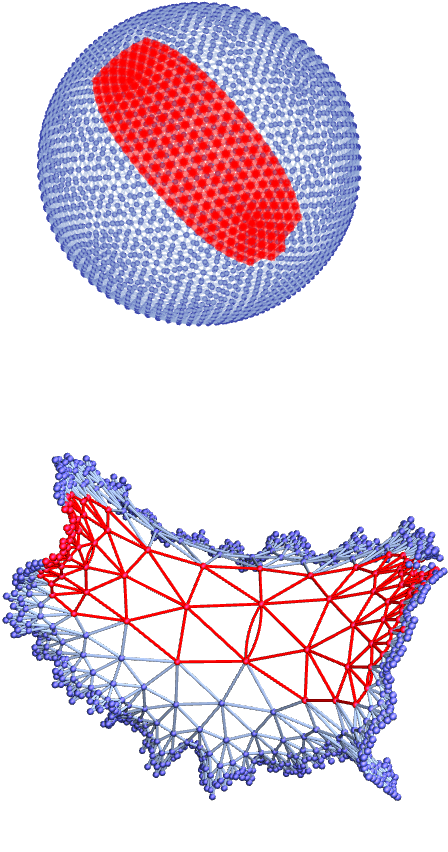
To construct an example, consider a graph formed from a mesh on the surface of an ellipsoid. (It is important that this mesh is intrinsic to the surface, with each mesh element corresponding to about the same surface area—and that the mesh does not just come from, say, a standard θ, ϕ coordinate grid.)
As a first step, consider balls of progressively larger radii at different points on the ellipsoid mesh graph:

In the region of higher curvature near the tip, the area of the ball for a given radius is smaller, reflecting higher values of the Ricci scalar curvature R there:
But now consider tubes around geodesics on the ellipsoid mesh graph. Instead of measuring the scalar curvature R, these instead in effect measure components of the Ricci tensor along these geodesics.
To measure all the components of the Ricci tensor, we could consider not just a tube but a bundle of geodesics, and we could look at the sectional curvature associated with deformations of the shape of this bundle. Or, as an alternative, we could consider tubes along not just one, but two geodesics through a given point. But in both cases, the analogy with the continuous case is easiest if we can identify something that we can consider an orthogonal direction.
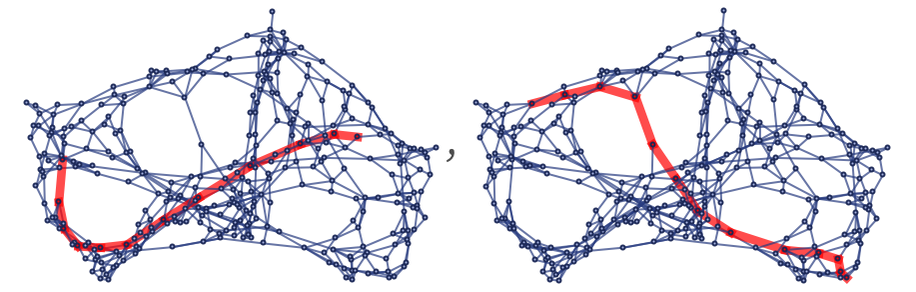
One way to do this on a graph is to start from a particular geodesic through a given point, then to look at all other geodesics through that point, and work out which ones are the largest graph distance away. These show sequences of progressively more distant geodesics (as measured by the graph distance to the original geodesic of their endpoints):



In general there may be many choices of these geodesics—and in a sense these correspond to different local choices of coordinates. But given particular choices of geodesics we can imagine using them to form a grid.
Looking at growth rates of volumes on this grid then gives us results not just about the Ricci tensor, but also about the Riemann tensor, about parallel transport and about covariant derivatives (cf. [27]).
The examples we have shown so far all involve graphs that have a straightforward correspondence with familiar geometry. But exactly the same methods can be used on the kinds of graphs and hypergraphs that arise from our models. This shows tubes of successively larger radii along two different geodesics:
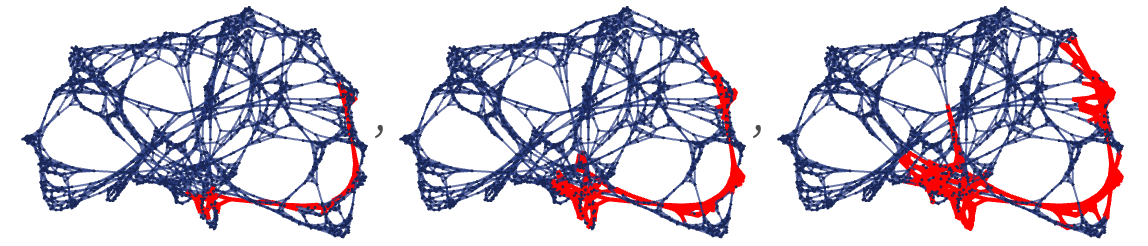
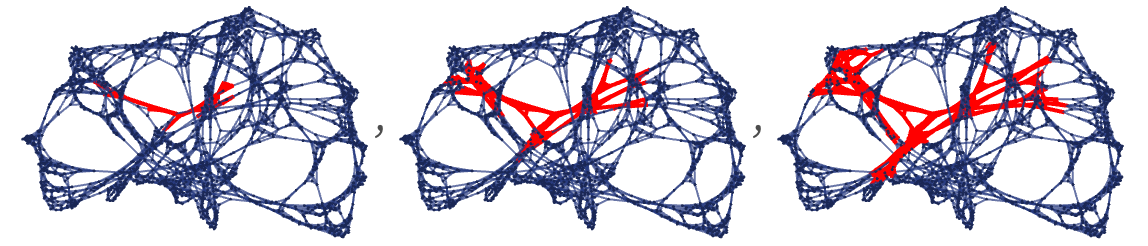
In the limit of a large number of steps, we can measure the volumes of tubes like these to compute approximations to projections of the Ricci tensor—and for example determine the level of isotropy of the emergent geometry of our models.
 download pdf
download pdf  ARXIV
ARXIV peer review
peer review