download pdf 
ARXIV
peer reviewHaving seen how our notion of dimension works in cases where we can readily recognize emergent geometry, we now turn to using it to study the more general limiting behavior of our models.
As a first example, consider the 22 42 rule
which generates results such as (with about 1.84t relations at step t):
If we attempt to reconstruct a surface from successive steps in the evolution of this rule, no clearly recognizable geometry emerges:
But instead we can try to characterize the results using Vr(X) and our notion of dimension. We compute Vr(X) as we do elsewhere: by starting at a point in the structure and constructing successively larger balls:
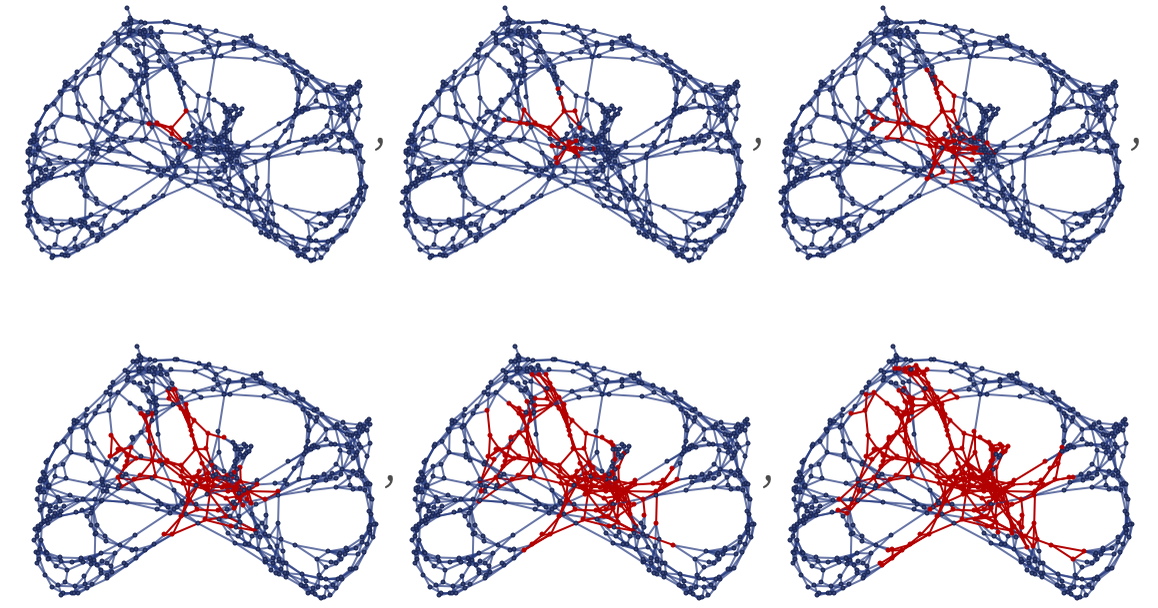
Computing the Δ(r) for all points over the first 16 steps of evolution gives:
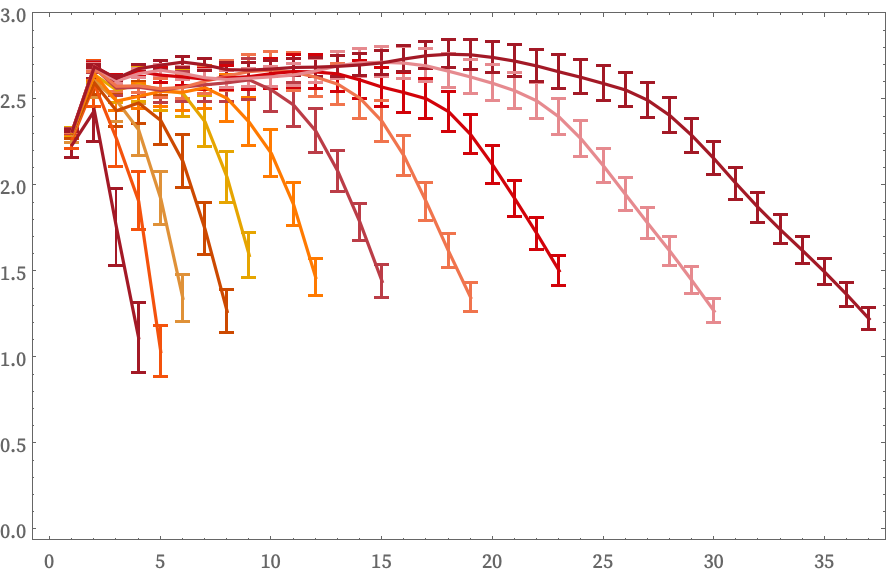
The most important feature of this plot is that it suggests Δ(r) might approach a definite limit as the number of steps increases. And from the increasing region of flatness there is some evidence that perhaps Vr might approach a stable rd form, with d ≈ 2.7, suggesting that in the limit this rule might produce some kind of emergent geometry with dimension around 2.7.
What about other rules? Here are some examples for rules we have discussed above:
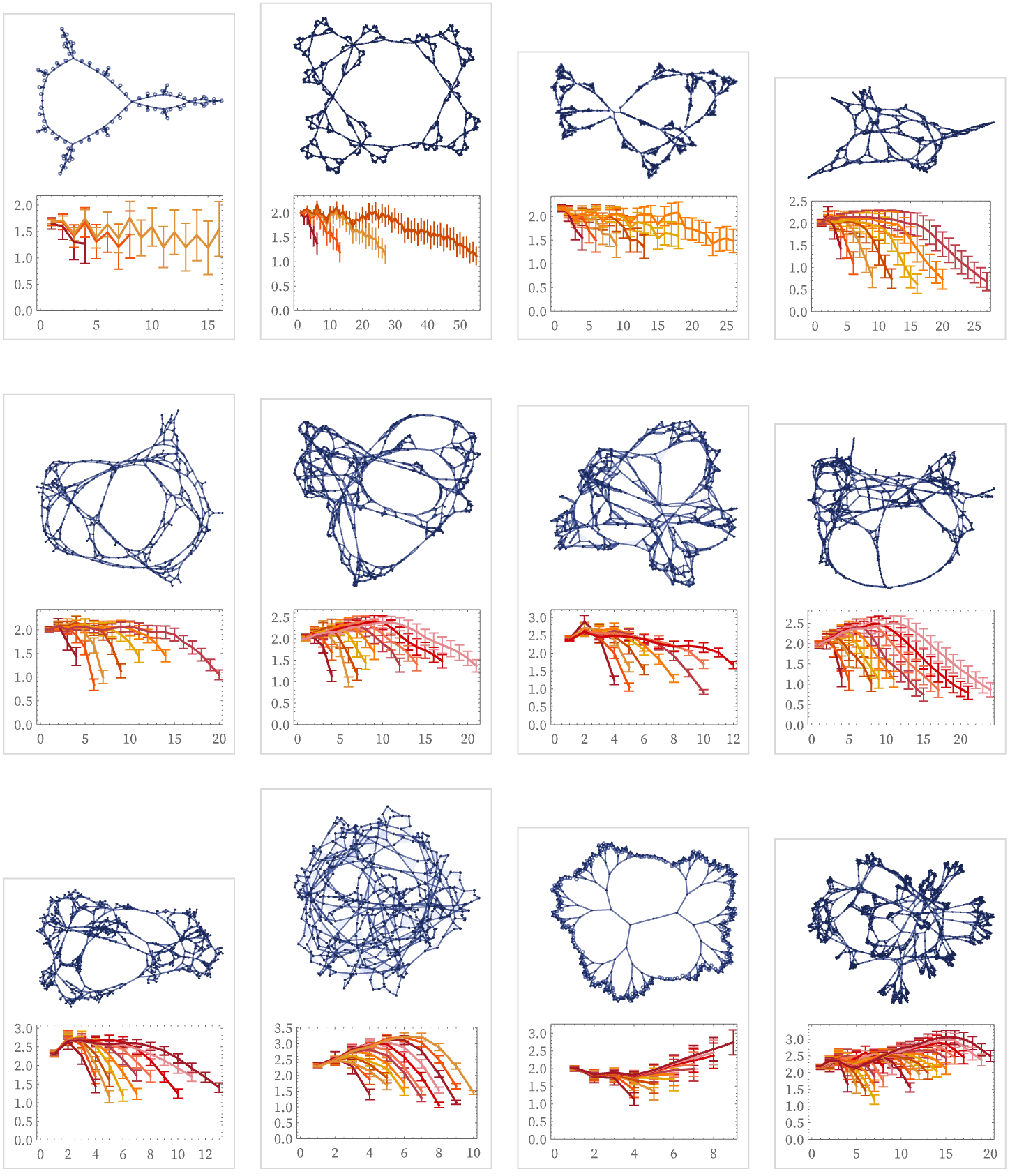
Some rules do not show convergence, at least over the number of steps sampled here. Other rules show quite stable limiting forms, often with a flat region which suggests a structure with definite dimension. Sometimes this dimension is an integer, like 1 or 2; often it is not. Still other rules seem to show linear increase in log differences of Vr, implying an exponential form for Vr itself, characteristic of tree-like behavior.