At the lowest level, the structures on which our models operate consist of collections of relations between identical (but labeled) discrete elements. One convenient way to represent such structures is as graphs (or, in general, hypergraphs). The elements are the nodes of the graph or hypergraph. The relations are the (directed) edges or hyperedges that connect these elements.
For example, the graph
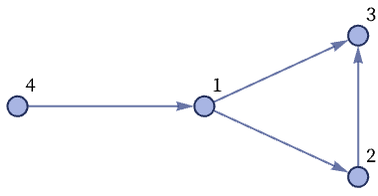
corresponds to the collection of relations
The order in which these relations are stated is irrelevant, but the order in which elements appear within each relation is considered significant (and is reflected by the directions of the edges in the graph). The specific labels used for the elements (here 1, 2, 3, 4) are arbitrary; all that matters is that a particular label always refer to the same element.
 download pdf
download pdf  ARXIV
ARXIV peer review
peer review