Having discussed the general correspondence between relativity and quantum mechanics suggested by our models, we can now consider the extreme situation of event horizons and singularities.
As we discussed above, an event horizon in spacetime corresponds in our models to disconnection in the causal graph: after some slice in our foliation in time, there is no longer causal connection between different parts of the system. As a result, even if the system is locally causal invariant, branch pairs whose products go on different sides of the disconnection can never resolve. The only way to make a foliation in which this does not happen is then effectively to freeze time before the disconnection occurs.
When there is a true disconnection in the causal graph, there is no choice about this. But it is also perfectly possible just to imagine setting up a coordinate system that freezes time in a particular region of space—although it will typically take more and more effort (and energy) to consistently maintain such a coordinate singularity as other parts of the system evolve.
But now there is an interesting correspondence with quantum measurement. As we discussed in 8.14, in the context of our models, one can view a quantum measurement (or a “collapse of the wave function”) as being associated with a foliation that freezes time for the state that is the outcome of the measurement. In essence, therefore, quantum measurement corresponds to having a coordinate singularity in a particular region of branchial space.
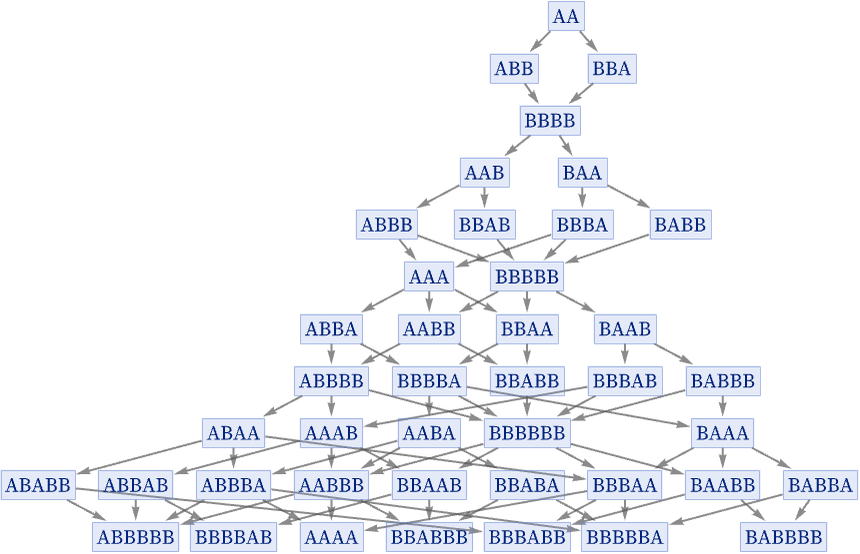
What about an event horizon? As we saw above, one way in which an event horizon can occur is if some branch of the multiway system simply terminates, so that in a sense time stops for it. Another possibility is that—at least temporarily—there can be a disconnected piece in the branchial graph. Consider for example the (causal invariant) string substitution system:
The multiway system for this rule is
and the branchial graph shows temporary disconnections
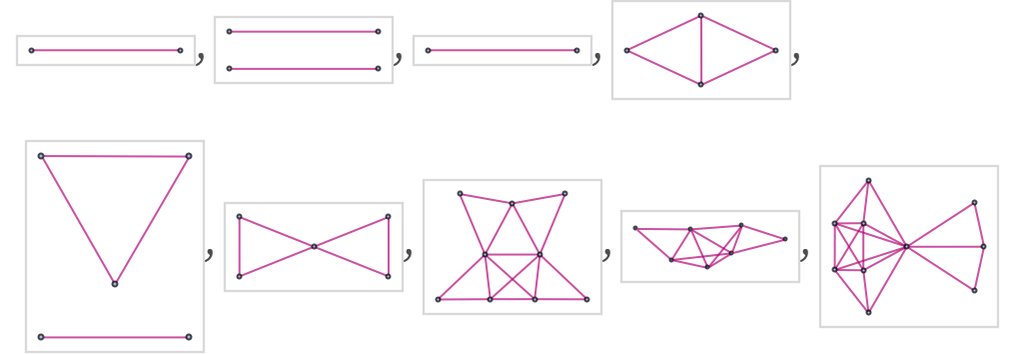
although the “spacetime” causal graph stays connected:

One can think of these temporary disconnections in the branchial graphs as corresponding to isolated regions of branchial space where entanglement at least temporarily cannot occur—and where some pure quantum state (such as qubits) can be maintained, at least for some period of time.
In some sense, one can potentially view such disconnections as being like black holes in branchial space. But the continued generation of branch pairs (in a potential analog to Hawking radiation [129]) causes the “black hole” to dissipate.
A different situation can occur when there is also disconnection in the causal graph—leading in our models to disconnection in the spatial hypergraph—and thus a spacetime event horizon. As a simple example, consider the string substitution system (starting from AA):
The causal graph in this case is
and the sequence of branchial graphs (with the standard foliation) is:
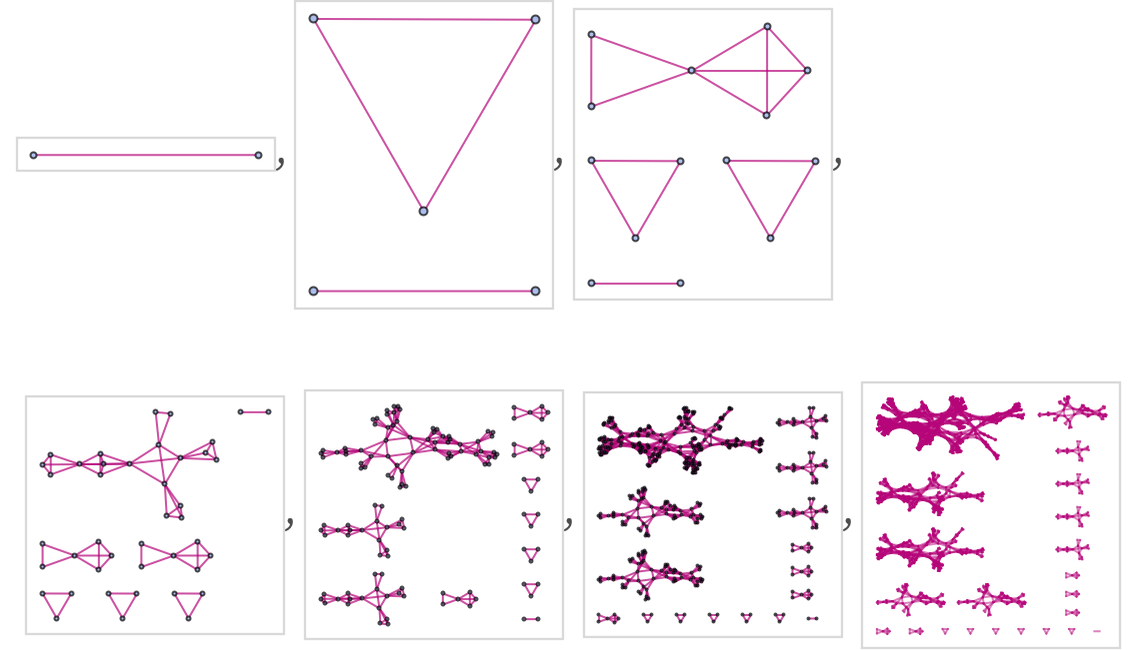
What has happened here is that there are event horizons both in physical space and in branchial space.
We can expect similar phenomena in our full models, and extrapolating this to a physical black hole what this represents is the presence of both a causal event horizon (associated with motion in space, propagation of light, etc.) and an entanglement event horizon (associated with quantum entanglement). The causal event horizon will be localized in physical space (say at the Schwarzschild radius [130]); the entanglement event horizon can be considered instead to be localized in branchial space.
It should be noted that these horizons are in a sense linked through the multiway causal graph, which in the example above initially has the form
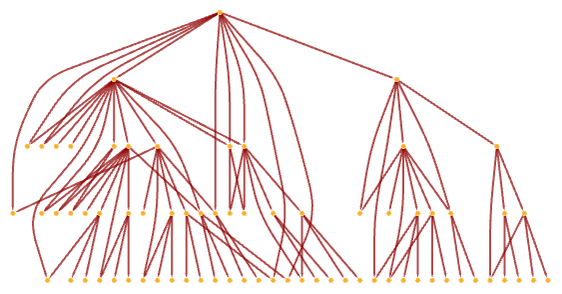
and after more steps builds up the structure:

In this graph, there are both spacelike and branchlike connections, and here both of them exhibit disconnection, and therefore event horizons. And even though the geometrical structure of branchial space is very different from physical space, there are potentially further correspondences to be made between them. For example, while the speed of light c governs the maximum spacelike speed, the maximum entanglement rate ζ that we introduced above governs the maximum “branchlike speed”, or entanglement rate.
When a disconnection occurs in the spacetime causal graph (and thus the spatial hypergraph), we can think of this as implying that geodesics in spacetime would have to exceed c in order not to be trapped. When a disconnection occurs in the branchial graph, we can think of geodesics having to “exceed speed ζ” in order not to be trapped.
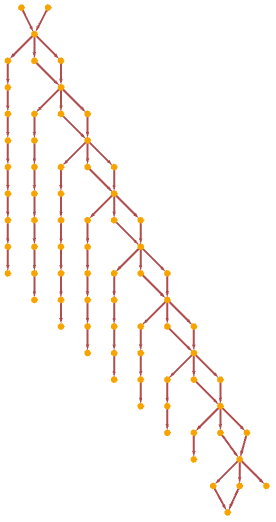
It is worth pointing out that the analog of a true singularity—and not just an event horizon—can occur in our models if there are paths in the multiway system that simply terminate, as for B, BB, etc. in:
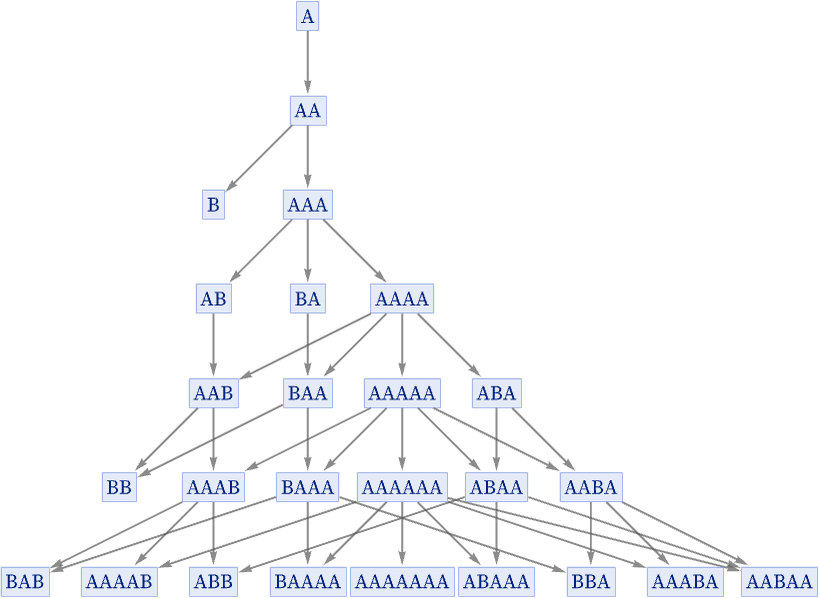
When this happens, there are many geodesics that in effect converge to a single point, like in spacetime singularities in general relativity. Here, however, we see that this can happen not only in physical space, but also in the multiway system, or, in other words, in branchial space. (In our systems, it is probably the case that singularities must be enclosed in event horizons, in the analog of the cosmic censorship hypothesis.)
Many results from general relativity can presumably be translated to our models, and can apply both to physical space and branchial space (see [121]). In the case of a black hole, our models suggest that not only may a causal event horizon form in physical space; also an entanglement horizon may form in branchial space. One may then imagine that quantum information is trapped inside the entanglement horizon, even without crossing the causal event horizon—with implications perhaps similar to recent discussions of resolutions to the black hole quantum information problem [131][132][133].
There is a simple physical picture that emerges from this setup. As we have discussed, quantum measurement can be thought of as a choice of coordinates that “freeze time” for some region in branchial space. For an observer close to the entanglement horizon, it will not be possible to do this. Much like an observer at a causal event horizon will be stretched in physical space, so also an observer at an entanglement horizon will be stretched in branchial space. And the result is that in a sense the observer will not be able to “form a classical thought”: they will not successfully be able to do a measurement that definitively picks the branch of the multiway system in which something fell into the black hole, or the one in which it did not.
 download pdf
download pdf  ARXIV
ARXIV peer review
peer review