In our models, the passage of time basically corresponds to the progressive updating of the hypergraph. Time is therefore fundamentally computational: its passage reflects the performance of a computation—and typically one that is computationally irreducible. It is notable that in a sense the progression of time is necessary even to maintain the structure of space. And this effectively forces the entropic arrow of time (reflected in the effective randomization associated with irreducible computation) to be aligned with the cosmological arrow of time (defined by the overall evolution of the structure of space).
At the outset, time in our models has a very different character from space. The phenomenon of causal invariance, however, implies a link which leads to relativistic invariance. To see this, we can begin much as in the traditional development of special relativity [111] by considering what constitutes a physically realizable observer. In our model, everything is represented by the evolving hypergraph, including all of the internal state of any observer. One consequence of this is that the only way an observer can “sense” anything about the universe is by some updating event happening within the observer.
And indeed in the end all that any observer can ultimately be sensitive to is the causal relationships between different updating events that occur. From a particular evolution history of a hypergraph, we can construct a causal graph whose nodes correspond to updating events, and whose directed edges represent the causal relations between these events—in the sense that there is an edge between events A and B if the input to B involves output from A. For the evolution shown above, the beginning of the causal graph is:
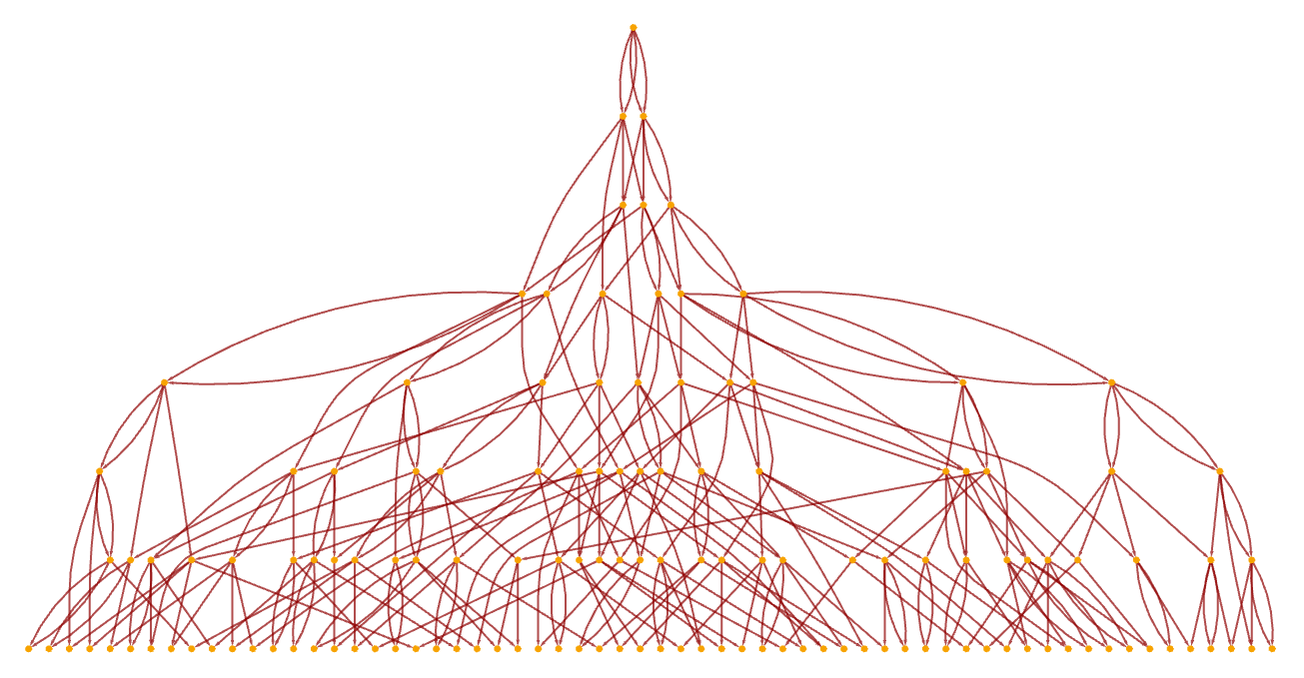
We can think of this causal graph as representing the evolution of our system in spacetime. The analog of a light cone is then the set of nodes that can be reached from a given node in the graph. Every edge in the graph represents a timelike relationship between events, and can be thought of as corresponding to a timelike direction in spacetime. Nodes that cannot be reached from each other by following edges of the graph can be thought of as spacelike separated. Just as for space with the “spatial hypergraphs” we discussed above, there is nothing in the abstract that defines the geometry of spacetime associated with the causal graph; everything must emerge from the pattern of connections in the graph, which in turn are generated by the operation of the underlying rules for our models.
In its original construction, a causal graph is in a sense a causal summary of a particular evolution history for a given rule, with a particular sequence of updating events. But when the underlying rule has the property of causal invariance, this has the important consequence that in the appropriate limit the causal graph obtained always has the same form, independent of the particular sequence of updating events. In other words, when there is causal invariance, the system in a sense always has a unique causal history.
The interpretation of this causal history in terms of a spacetime history, however, depends on what amount to definitions made by an observer. In particular, to define what can be interpreted as a time coordinate, one must set up a foliation of the causal graph, with successive slices corresponding to successive steps in time.
There are many such foliations that can be set up. The only fundamental constraint is that events in a given slice cannot be directly connected by an edge in the causal graph—or, in other words, they must be spacelike separated. The possible foliations thus correspond to possible sequences of spacelike hypersurfaces, analogous to those in standard discussions of spacetime.
(Note that the causal graph ultimately just defines a partial order on the set of events, and one could in principle imagine having arbitrarily complex foliations set up to imply any given total order of events. But such foliations are not realistic for macroscopic observers with bounded computational resources, and in our analysis of observable continuum limits we can ignore them.)
When one reaches a particular spacelike hypersurface, it represents a particular set of events having occurred, and thus a particular state of the underlying system having been reached, represented by a particular hypergraph. Different sequences of spacelike hypersurfaces thus correspond to different sequences of “instantaneous states” having been reached—corresponding to different evolution histories. But the crucial point is that causal invariance implies that even though the sequences of instantaneous states are different, the causal graphs representing the causal relationships between events that occur in them are always the same. And this is the essence of how the phenomena of relativistic invariance—and general covariance—are achieved.
 download pdf
download pdf  ARXIV
ARXIV peer review
peer review