Above we gave a brief summary of how quantum measurement can work in the context of our models. Here we give some more detail.
In a sense the key to quantum measurement is reconciling our notion that “definite things happen in the universe” with the formalism of quantum mechanics—or the branching structure of a multiway system.
But if definite things are going to happen, what might they be?
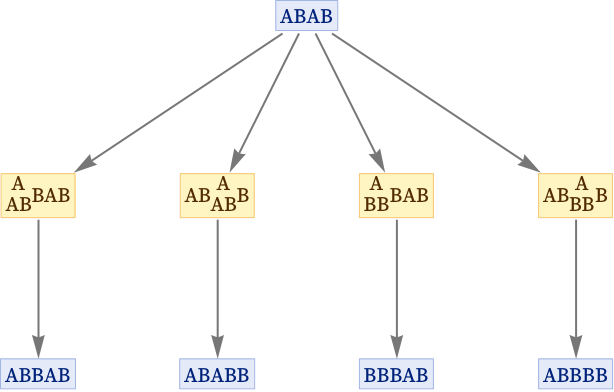
Here we will again consider the example of a string substitution system, although the core of what we say also applies to the full hypergraph case. Consider the rule
We could imagine a simple “classical” procedure for evolving according to this rule, in which we just do all updates we can (say, based on a left-to-right scan) at each step:
But in fact we know that there are many other possibilities, that can be represented by the multiway system:
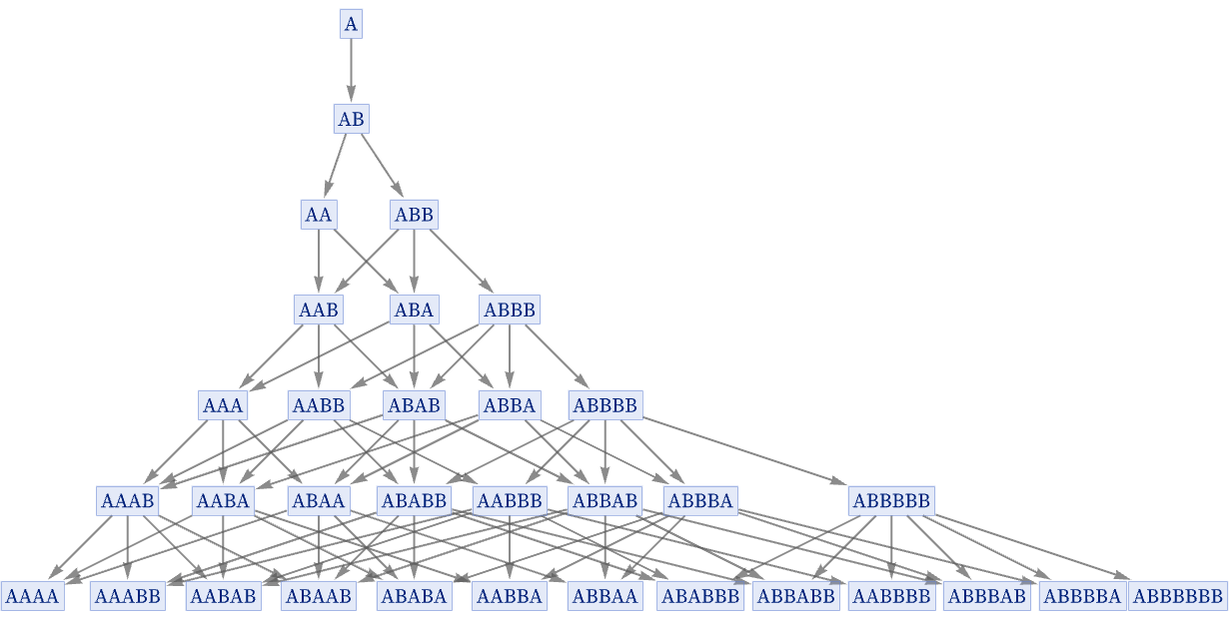
Most of the states that appear in the multiway system are, however, “unfinished”, in the sense that there are additional “independent” updates that can consistently be done on them. For example, with the rule {A BA} there are 4 separate updates that can be applied to AAAA:
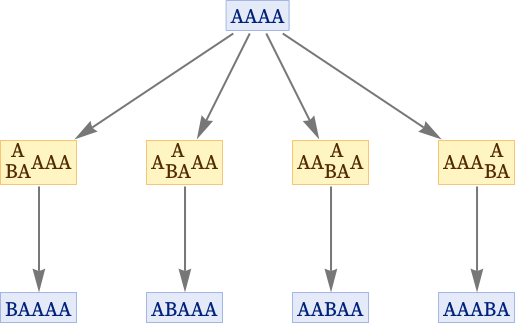
But none of these depend on the others, so they can in effect all be done together, giving the result BABABABA.
Put another way, all of these updates involve “spacelike separated” parts of the string, so they are all causally independent, and can all consistently be carried out at the same time. As discussed in 5.21, doing all updates across a state together can be thought of as evolving a system in “generational steps” to produce “generational states”.
In some multiway cases, there may be a single sequence of generational states:
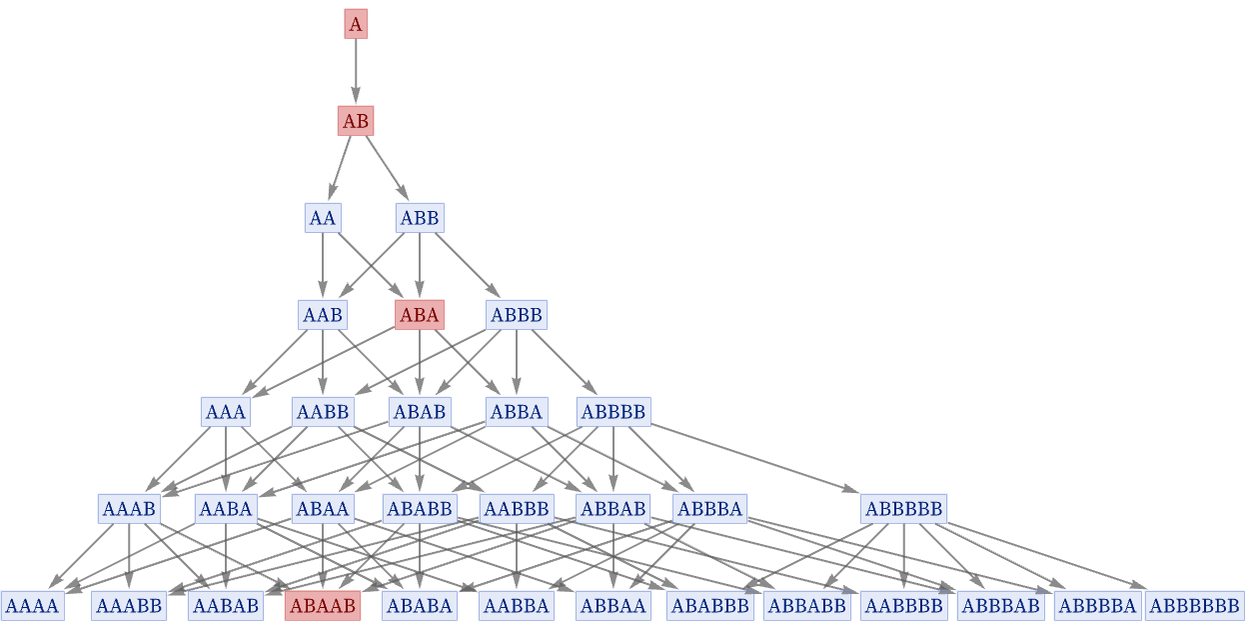
In other cases, there can be several branches of generational states:
The presence of multiple branches is a consequence of having a mixture of spacelike and branchlike separated events that can be applied to a single state. For example, with the rule {A AB, A BB} the first and second updates here are spacelike separated, but the first and third are branchlike separated:
A view of quantum measurement is that it is an attempt to describe multiway systems using generational states. Sometimes there may be a unique “classical path”; sometimes there may be several outcomes for measurements, corresponding to several generational states.
But now let us consider the actual process of doing an experiment on a multiway system—or a quantum system. Our basic goal is—as much as possible—to describe the multiway system in terms of a limited number of generational states, without having to track all the different branches in the multiway system.
At some point in the evolution of a string substitution system we might see a large number of different strings. But we can view them all as part of a single generational state if they in effect yield only spacelike separated events. In other words, if the strings can be assembled without “branchlike ambiguity” they can be thought of as forming a consistent generational state.
In the standard formalism of quantum mechanics, we can think of the states in the multiway system as being quantum states. The construct we form by “assembling” these states can be thought of as a superposition of the states. Causal invariance then implies that through the evolution of the multiway system any such superposition will then actually become a single quantum state. In some sense the observer “did nothing”: they just notionally identified a collection of states. It was the actual evolution of the system that produced the specific combined state.
In describing a quantum system—or a multiway system—one must in effect define coordinates, and in particular one must specify what foliation one is going to use to represent the progress of time. And this freedom to pick a “quantum observation frame” is critical in being able to maintain a view in which one imagines “definite things to happen” in the system.
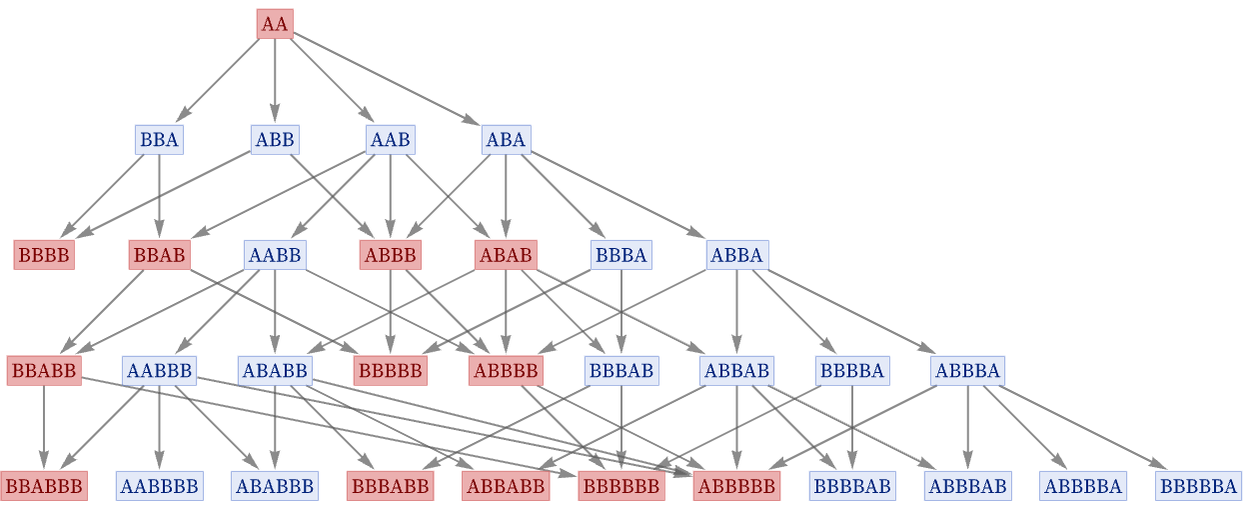
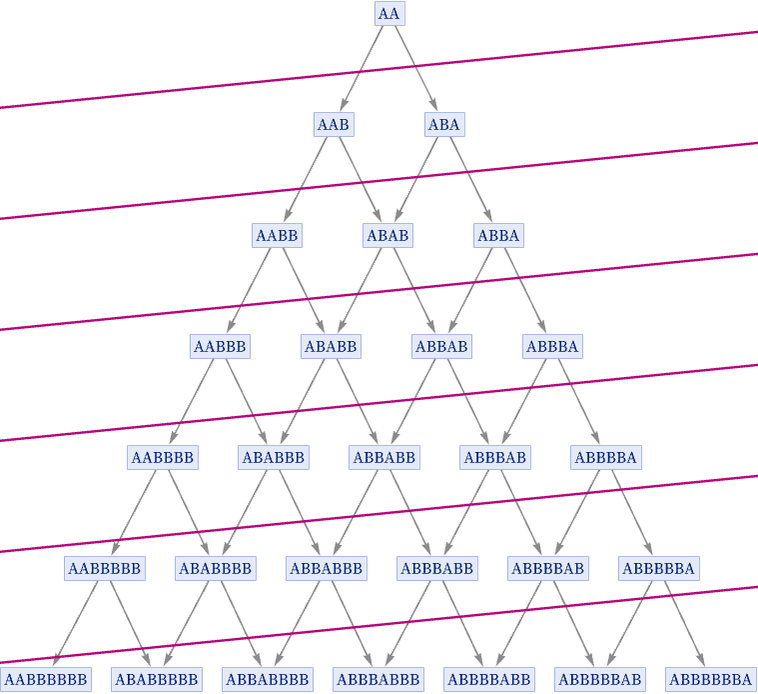
With a foliation like the following, at any given time there is a mixture of different states, and no attempt has been made to find a way to “summarize” what the system is doing:
Consider, however, a foliation like the following:
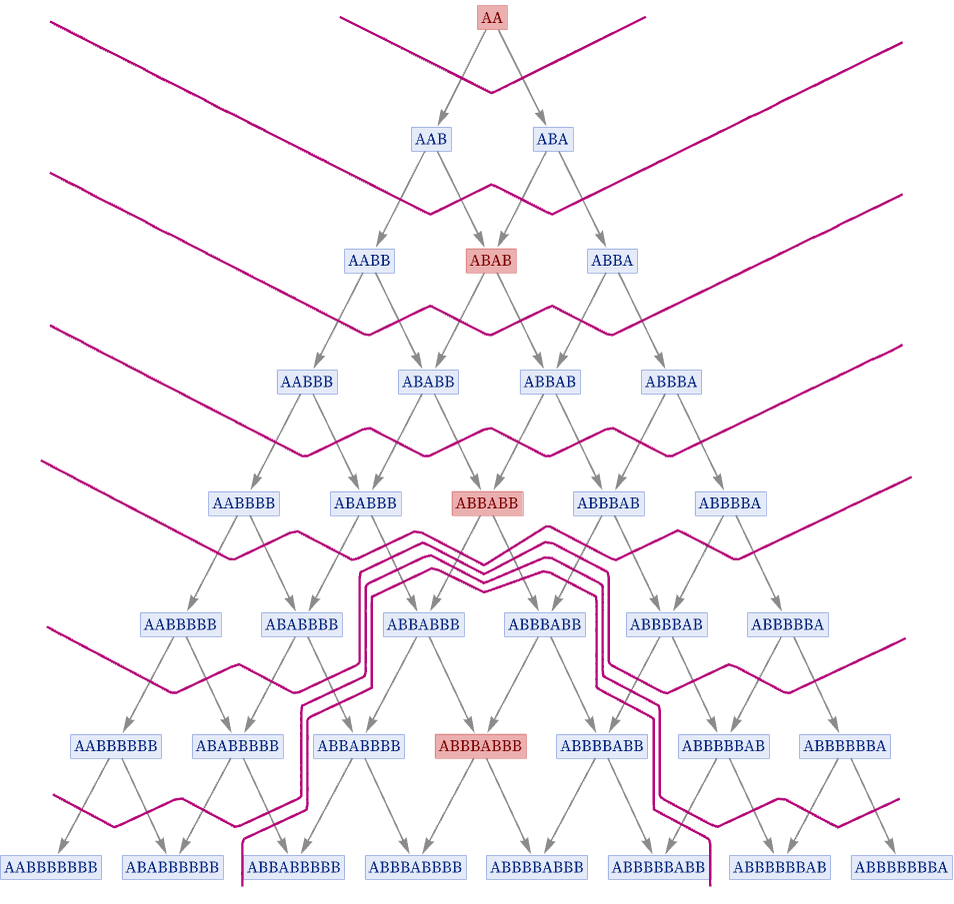
In this picture, generational states have been highlighted, and a foliation has been selected that essentially “freezes time” around a particular generational state. In effect, the observer is choosing a quantum observation frame in which there is a definite classical outcome for the behavior of the system.
“Freezing time” around a particular state is something an observer can choose to do in their description of the system. But the crucial point is that the actual dynamics of the evolution of the multiway system cause this choice to have implications.
In particular, in the case shown, the region of the multiway system in which “time is frozen” progressively expands. The choice the observer has made to freeze a particular state is causing more and more states to have to be considered as similarly frozen. In the physics of quantum measurement, one is used to the idea that for a quantum measurement to be considered to have a definite result, it must involve more and more quantum degrees of freedom. What we see here is effectively a manifestation of this phenomenon.
In freezing time in something like the foliation in the picture above what we are effectively doing is creating a coordinate singularity in defining our quantum observation frame. And there is an analogy to this in general relativity and the physics of spacetime. Just as we freeze time in our quantum frame, so also we can freeze time in a relativistic reference frame. For example, as an object approaches the event horizon of a black hole, its time as described by a typical coordinate system set up by an observer far from the black hole will become frozen—and just like in our quantum case, we will consider the state to stay fixed.
But there is a complicated issue here. To what extent is the singularity—and the freezing of time—a feature of our description, and to what extent is it something that “really happens”? This depends in a sense on the relationship one has to the system. In traditional thinking about quantum measurement, one is most interested in the “impressions” of observers who are in effect embedded in the system. And for them, the coordinate system they chose in effect defines their reality.
But one can also imagine being somehow “outside the system”. For example, one might try to set up a quantum experiment (or a quantum computer) in which the construction of the system somehow makes it natural to maintain a “frozen time” foliation. The picture below shows a toy example in which the multiway system by its very construction has a terminal state for which time does not advance:
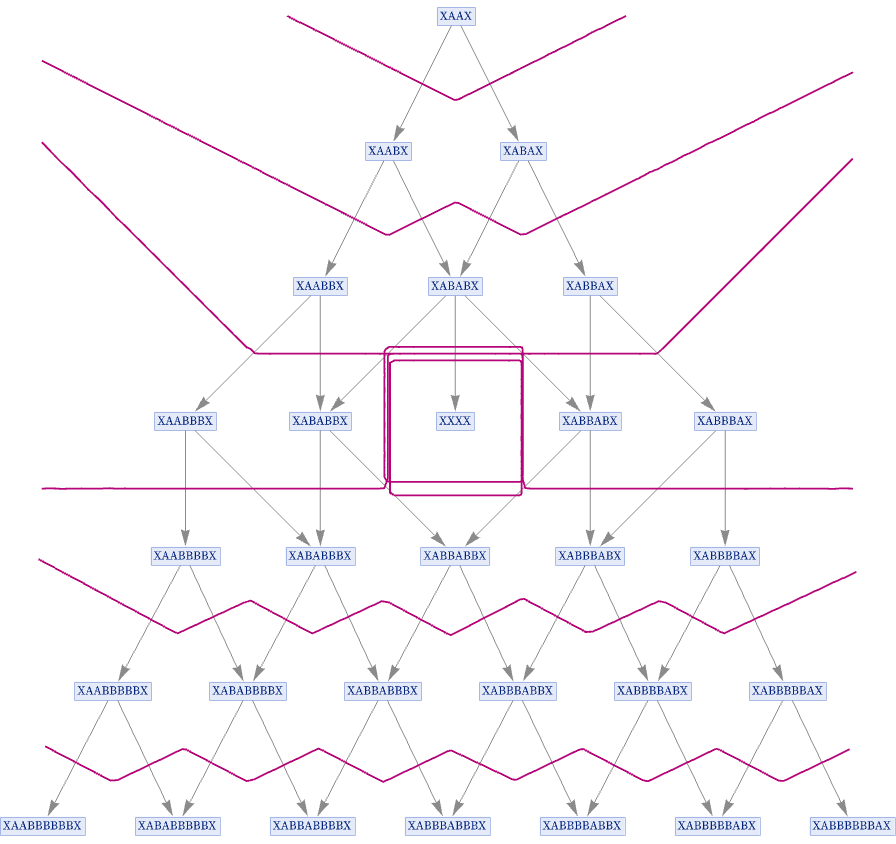
But now the question arises of what can be achieved in the multiway system corresponding to the actual physical universe. And here we can expect that one will not be able to set up truly isolated states, and that instead there will be continual inevitable entanglement. What one might have imagined could be maintained as a separate state will always become entangled with other states.
The picture below shows a slightly more realistic multiway system, with an attempt to construct a foliation that freezes time:
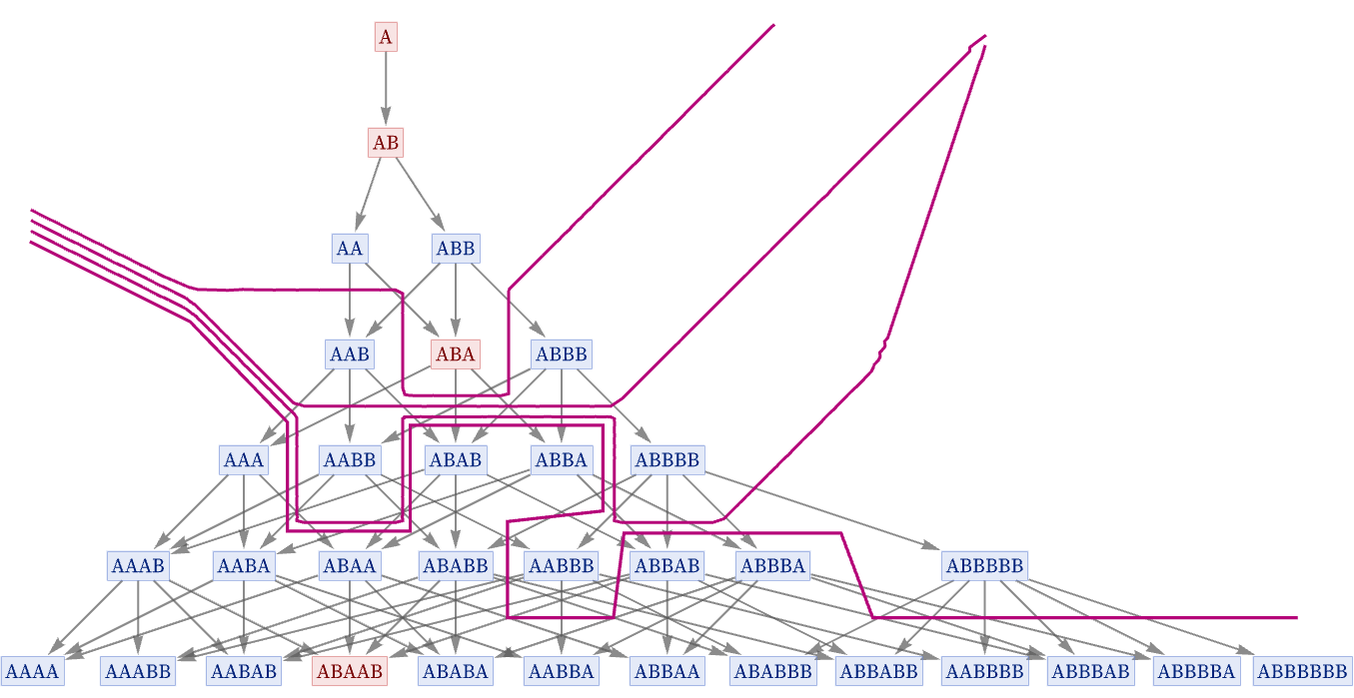
And what we see here is that in a sense the structure of the multiway graph limits the extent to which we can freeze time. In effect, the multiway system forces decoherence—or entanglement—just by its very structure.
We should note that it is not necessarily the case that there is just a single possible sequence of generational states, corresponding in a sense to a single possible “classical path”. Here is an example where there are four generational states that occur at a particular generational step. And now we can for example construct a foliation that—at least for a while—“freezes time” for all of these generational states:
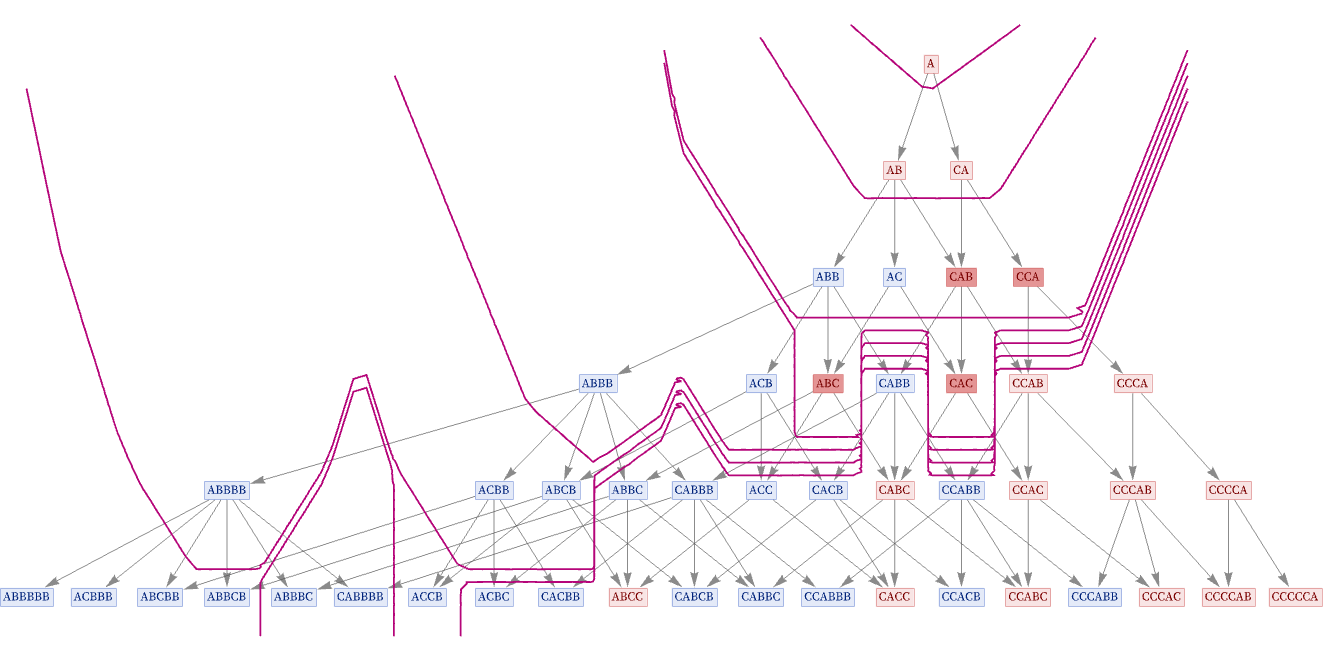
It is worth pointing out that if we try to freeze time for something that is not a proper generational state, there will be an immediate issue. A proper generational state contains the results of all spacelike separated events at a particular point in the evolution of a system. So when we freeze time for it, we are basically allowing other branchlike separated events to occur, but not other spacelike separated ones. However, if we tried to freeze time for a state that did not include all spacelike separated events, there would quickly be a mismatch with the progress of time for the excluded events—or in effect the singularity of quantum observation frame would “spill over” into a singularity in the causal graph, leading to a singularity in spacetime.
In other words, the fact that the states that appear in quantum measurement are generational states is not just a convenience but a necessity. Or, put another way, in doing a quantum measurement we are effectively setting up a singularity in branchial space, and only if the states we measure are in effect “complete in spacetime” will this singularity be kept only in branchial space; otherwise it will also become a singularity in physical spacetime.
In general, when we talk about quantum measurement, we are talking about how an observer manages to construct a description of a system that in effect allows the observer to “make a conclusion” about what has happened in the system. And what we have seen is that appropriate “time-freezing foliations” allow us to do this. And while there may be some restrictions, it is usually in principle possible to construct such foliations in a multiway system, and to have them last as long as we want.
But in practice, as the pictures above begin to suggest, after a while the foliations we have to construct can get increasingly complicated. In effect, what we are having to do in constructing the foliation is to “reverse engineer” the actual evolution of the multiway system, so that with our elaborate description we are still managing to maintain time as frozen for a particular state, carefully avoiding complicated entanglements that have built up with other states.
But there is a problem here. Because in effect we are asking the observer to “outcompute” the system itself. Yet we can expect that the evolution of the multiway system, say for one of our models, will usually correspond to an irreducible computation. And so we will be asking the observer to do a more and more elaborate computation to maintain the description they are using. And as soon as the computation required exceeds the capability of the observer, the observer will no longer be able to maintain the description, and so decoherence will be inevitable.
It is worthwhile to compare this situation with what happens in thermodynamic processes, and in particular with apparent entropy increase. In a reversible system, it is always in principle possible to recognize, say, that the initial conditions for the systems were simple (and “low entropy”). But in practice the actual configurations of the system usually become complicated enough that this is increasingly difficult to do. In traditional statistical mechanics one talks of “coarse-grained” measurements as a way to characterize what an observer can actually analyze about a system.
In computational terms we talk about the computational capabilities of the observer, and how computational irreducibility in the evolution of the system will eventually overwhelm the computational capabilities of the observer, making apparent entropy increase inevitable [1:9.3].
In the quantum case, we now see how something directly analogous happens. The analog of coarse graining is the effort to create a foliation with a particular apparent outcome. But eventually this becomes infeasible, and—just like in the thermodynamic case—we in effect see “thermalization”, which we can now attribute to the effects of computational irreducibility.
 download pdf
download pdf  ARXIV
ARXIV peer review
peer review