8.15 Operators in Quantum Mechanics

In standard quantum formalism, there are states, and there are operators (e.g. [125]). In our models, updating events are what correspond to operators. In the standard evolution of the multiway system, all applicable operators are in effect “automatically applied” to every state to generate the actual evolution of the system. But to understand the correspondence with standard quantum formalism, we can imagine just applying particular operators by doing only particular updating events.

Consider the string substitution system:

In this system we effectively have two operators O₁ and O₂, corresponding to these two possible updating rules. We can think about building up an operator algebra by considering the relations between different sequences of applications of these operators.

In particular, we can study the commutator:

[O₁,O₂] = O₁O₂ – O₂O₁

In terms of the underlying rules, this commutator corresponds to:

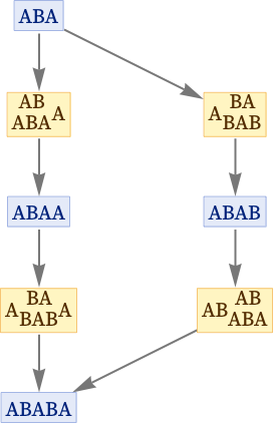
At the first step, the results of applying O₁ and O₂ to the initial state are different, and we can say that the states generated form a branch pair. But then at the second step, the branch pair resolves, and the branches merge to the same state. In effect, we can represent this by saying that O₁ and O₂ commute, or that:

[O₁,O₂] = O₁O₂ – O₂O₁ = 0

In general, there is a close relationship between causal invariance—and its implication for the resolution of all branch pairs—and the commuting of operators. And given our discussion above this should not be considered surprising: as we discussed, when there is causal invariance, it means that all branches can resolve to a single (“classical”) state, just like in standard quantum formalism the commuting of operators is associated with seemingly classical behavior.

But there is a key point here: even if causal invariance implies that branch pairs (and similarly commutators) will eventually resolve, they may take time to do so. And it is this delay in resolution that is the core of what leads to what we normally think of as quantum effects.

Once a branch pair has resolved, there are no longer multiple branches, and a single state has emerged. But before the branch pair has resolved, there are multiple states, and therefore what one might think of as “quantum indeterminacy”.

In the case where a branch pair has not yet resolved, the corresponding commutator will be nonzero—and in a sense the value of the commutator measures the branchlike distance between the states reached by applying the two different updates (corresponding to the two different operators).

In our model for spacetime, if a single event in the causal graph is connected in the causal graph to two different events we can ask what the spacelike separation of these events might be, and we might suppose that this spatial distance is determined by the speed of light c (say multiplied by the elementary time corresponding to traversal of the causal edge).

In thinking now about the multiway system, we can ask what the branchlike separation of states in a branch pair might be. This will now be a distance on a branchial graph—or effectively a distance in state space—and we can suppose that this distance is determined by ℏ. And depending on our conventions for measuring branchial distance, we might introduce an i, yielding a setup very much aligned with traditional quantum formalism.

Another interpretation of the non-commuting of operators is connected to the entanglement of quantum states. And here we now have a very direct picture of entanglement: two states are entangled if they are part of the same unresolved branch pair, and thus have a common ancestor.

The multiway graph gives a full map of all entanglements. But at any particular time (corresponding to a particular slice of a foliation defined by a quantum observation frame), the branchial graph gives a snapshot that captures the “instantaneous” configuration of entanglements. States closer on the branchial graph are more entangled; those further apart are less entangled.

It is important to note that distance on the branchial graph is not necessarily correlated with distance on the spatial graph. If we look at events, we can use the multiway causal graph to give a complete map of all connections, involving both branchlike and spacelike (as well as timelike) separations. Ultimately, the underlying rule determines what connections will exist in the multiway causal graph. But just as in the standard formalism of quantum mechanics, it is perfectly possible for there to be entanglement of spacelike-separated events.