5.6 The Frequency of Causal Invariance

The plots below show the fractions of rules found to be totally causal invariant [66], as a function of the total number of elements they involve, for the cases of k = 2 (A, B) and k = 3 (A, B, C):

\ CloudGet["https://wolfr.am/Ll9GSRbb"]

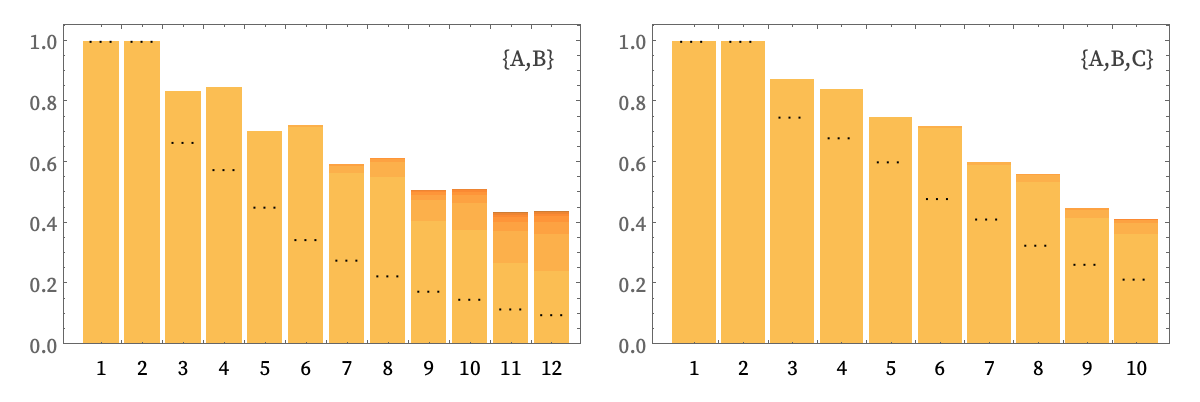
The darker colors indicate larger numbers of steps to resolve branch pairs. (There is some uncertainty in these plots—conceivably as much as 9% for 10 total elements with k = 3—since in some cases the states graph became too big to compute before it could be determined whether all branch pairs resolved.)

The dotted lines indicate rules are in a sense inevitably causal invariant because their left-hand sides involve strings that do not overlap themselves or each other, thereby guaranteeing total causal invariance. Rules such as AA  AAA are causal invariant despite having overlapping left-hand sides because their right-hand sides in a sense give the same result whatever overlap occurs.

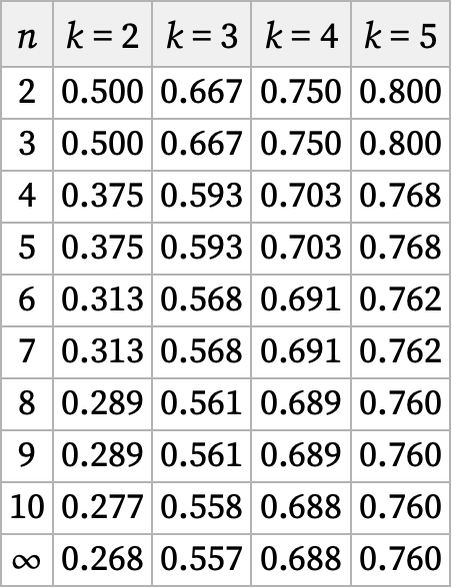
Ignoring the structure of rules, one can just ask what fraction of strings are non-overlapping [67]. Out of the total of kⁿ possible strings with length n containing k distinct elements the number that do not overlap themselves is given by [1:p1033]:

a[0] = 1; a[n_] := k a[n - 1] - If[EvenQ[n], a[n/2], 0]

This yields the following fractions (for the limit see e.g. [68][11:A003000]):

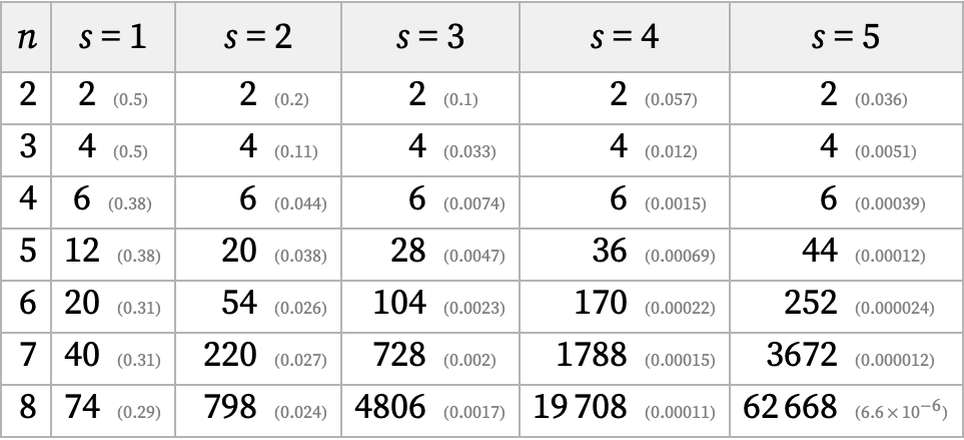
Grid[Module[{a}, a[0, _] = 1; a[n_, k_] := k a[n - 1, k] - If[EvenQ[n], a[n/2, k], 0]; Prepend[Append[ Table[Prepend[Table[N[a[n, k]/k^n, 3], {k, 2, 5}], n], {n, 2, 10}], Flatten[{Infinity, Table[N[a[200, k]/k^200, 3], {k, 2, 5}]}]], Item[Style[Text[TraditionalForm[#]]], Alignment -> Center] & /@ Prepend[Style[HoldForm[k = #], AutoSpacing -> True] & /@ Range[2, 5], HoldForm[n]]]], Frame -> All, FrameStyle -> GrayLevel[.7], Background -> {None, {GrayLevel[.94], White}}, BaseStyle -> "Text"]

One can also look at how many possible sets of s strings of length up to n allow no overlaps with themselves or each other [1:p1033]. The numbers and fractions for k = 2 are as follows:

results = <|{1, 1} -> 2, {1, 2} -> 3, {1, 3} -> 4, {1, 4} -> 5, {1, 5} -> 6, {2, 1} -> 2, {2, 2} -> 2, {2, 3} -> 2, {2, 4} -> 2, {2, 5} -> 2, {3, 1} -> 4, {3, 2} -> 4, {3, 3} -> 4, {3, 4} -> 4, {3, 5} -> 4, {4, 1} -> 6, {4, 2} -> 6, {4, 3} -> 6, {4, 4} -> 6, {4, 5} -> 6, {5, 1} -> 12, {5, 2} -> 20, {5, 3} -> 28, {5, 4} -> 36, {5, 5} -> 44, {6, 1} -> 20, {6, 2} -> 54, {6, 3} -> 104, {6, 4} -> 170, {6, 5} -> 252, {7, 1} -> 40, {7, 2} -> 220, {7, 3} -> 728, {7, 4} -> 1788, {7, 5} -> 3672, {8, 1} -> 74, {8, 2} -> 798, {8, 3} -> 4806, {8, 4} -> 19708, {8, 5} -> 62668|>; totalcases[n_, s_] := Binomial[2^n + s - 1, s]; Grid[Prepend[ Table[Prepend[ Table[With[{u = First[Lookup[results, {{n, s}}]]}, Row[{u, " ", Style[Row[{"(", NumberForm[N[u/totalcases[n, s]], 2], ")"}], Gray, 9]}]], {s, 5}], n], {n, 2, 8}], Item[Style[Text[TraditionalForm[#]]], Alignment -> Center] & /@ Prepend[Style[HoldForm[s = #], AutoSpacing -> True] & /@ Range[5], HoldForm[n]]], Frame -> All, FrameStyle -> GrayLevel[.7], Alignment -> {Flatten[{{Top, Center}, Table[" ", 7]}]}, Background -> {None, {GrayLevel[.94], White}}, BaseStyle -> "Text"]

To get a sense of the distribution of non-overlapping strings, one can make an array that shows which pairs of strings (ordered lexicographically) do not allow overlaps. Here are the results for k = 2 and k = 3 for strings respectively up to length 6 and length 4, showing clear structure in the space of possible strings [51]:

{ArrayPlot[ 1 - Boole[ Outer[ResourceFunction["StringOverlapsQ"][{#1, #2}] &, #, #] &@ Catenate[ Table[ResourceFunction["StringTuples"]["AB", n], {n, 2, 6}]]]], ArrayPlot[ 1 - Boole[ Outer[ResourceFunction["StringOverlapsQ"][{#1, #2}] &, #, #] &@ Catenate[ Table[ResourceFunction["StringTuples"]["ABC", n], {n, 2, 4}]]]]}