In addition to enumerating rules, we can also consider enumerating possible initial conditions. Like each side of a rule, these can be characterized by sequences n1k1n2k2... which give the number of relations ni of arity ki.
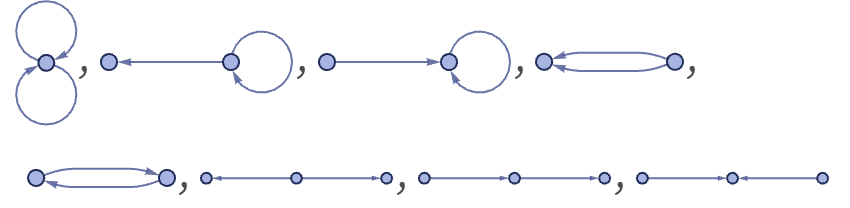
The only possible inequivalent 12 initial conditions are {{1,1}}, corresponding a graph consisting of a single self-loop, and {{1,2}}, consisting of a single edge. The possible inequivalent connected 22 initial conditions are:
These correspond to the graphs:
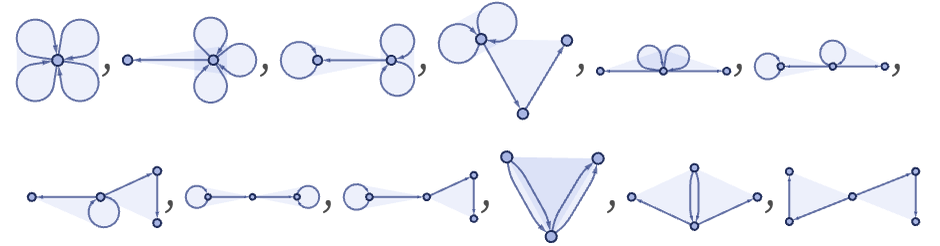
The possible inequivalent 13 initial conditions are:
These correspond to the hypergraphs:

There are 102 inequivalent connected 23 initial conditions. Ignoring ordering of relations, these correspond to hypergraphs with the following structures:
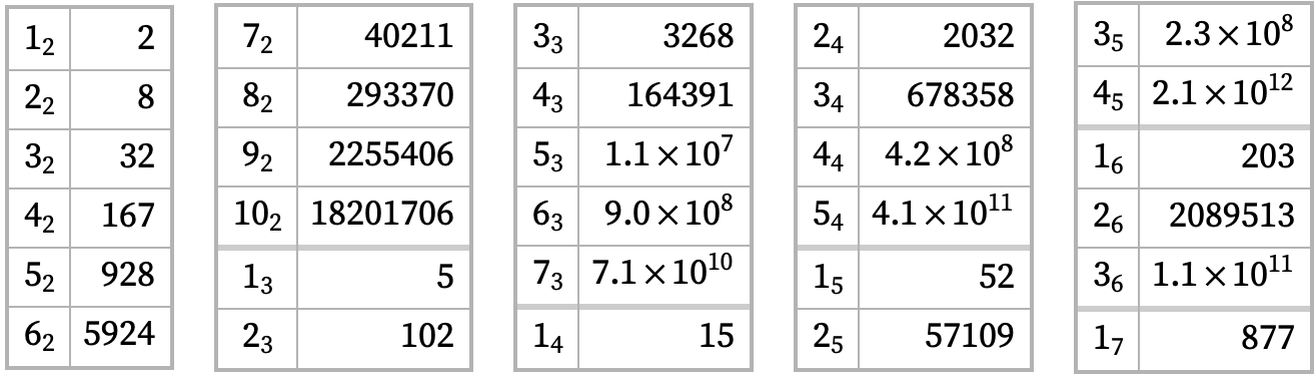
Ignoring connectivity, the number of possible inequivalent n1 initial conditions is PartitionsP[n], the number of 1n ones is BellB[n], while the number of n2 ones can be derived using cycle index polynomials (see also [11:A137975]). The number of inequivalent connected initial conditions for various small signatures is as follows (with essentially the same Bell number estimates applying as for rules) [12]:
A rule can only apply to a given initial condition if the initial condition contains at least enough relations to match all elements of the left-hand side of the rule. In other words, for a rule with signature nk … there must be at least n k-ary relations in the initial condition.
One way to guarantee that a rule will be able to apply to an initial condition is to make the initial condition in effect be a copy of the left-hand side of the rule, for example giving an initial condition {{1,2},{1,3}} for a rule with left-hand side {{x,y},{x,z}}. But the initial condition that in effect has the most chance to match is what is in many ways the simplest possible initial condition: the “self-loop” one where all elements are identical, or in this case {{0,0},{0,0}}. In what follows we will usually use such self-loop initial conditions Table[0,n,k].
 download pdf
download pdf  ARXIV
ARXIV peer review
peer review