In the traditional formalism of physics, the principles of special relativity are in a sense introduced as axioms, and then their consequences are derived. In our models, what amount to these principles can in effect emerge directly from the models themselves, without having to be introduced from outside.
To see how this works, consider the phenomenon of motion. In standard physics, one thinks of different states of uniform motion as corresponding to different inertial reference frames (e.g. [111][112]). These different reference frames in turn correspond to different choices of sequences of spacelike hypersurfaces, or, in our setup, different foliations of the causal graph.
As a simple example, consider the string substitution system BA AB, starting from ...BABABA... The causal graph for the evolution of this system can be drawn as a grid:
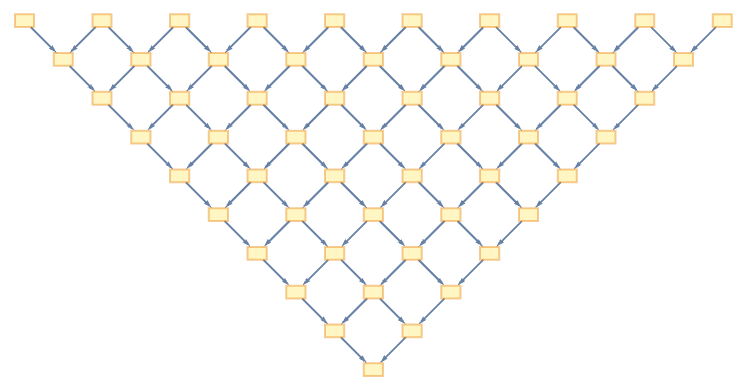
A simple foliation is just to form successive layers:
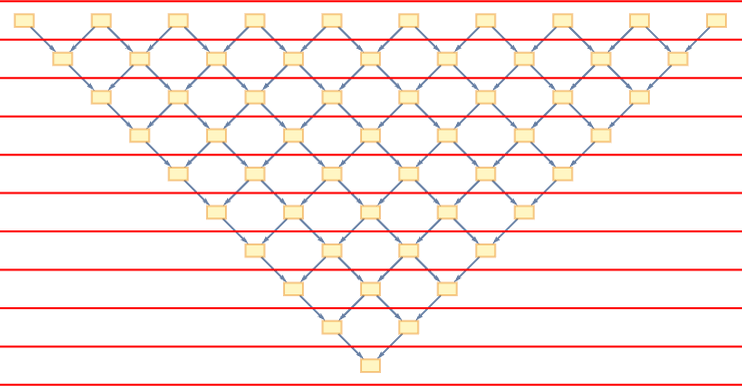
With this foliation, the sequence of states in the underlying string substitution system is:

In drawing our foliation of the causal graph, we can think of time as being vertical, and space horizontal. Now imagine we want to represent uniform motion. We can do this by making our foliation use slices with a slope proportional to velocity:
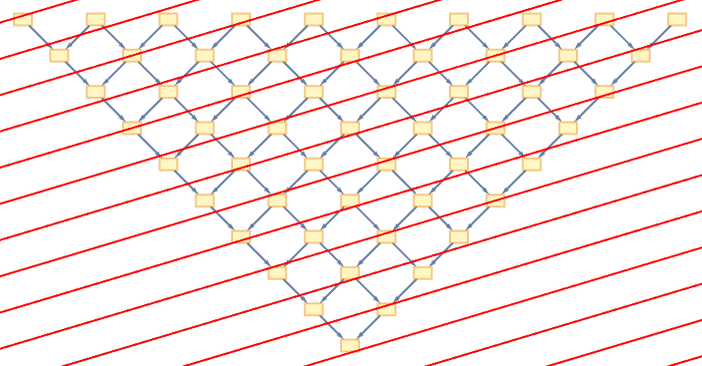
But imagine we want to show time vertically, while not destroying the partial order in our causal network. The unique way to do it (if we want to preserve straight lines) is to transform a point {t,x} to ![]() :
:
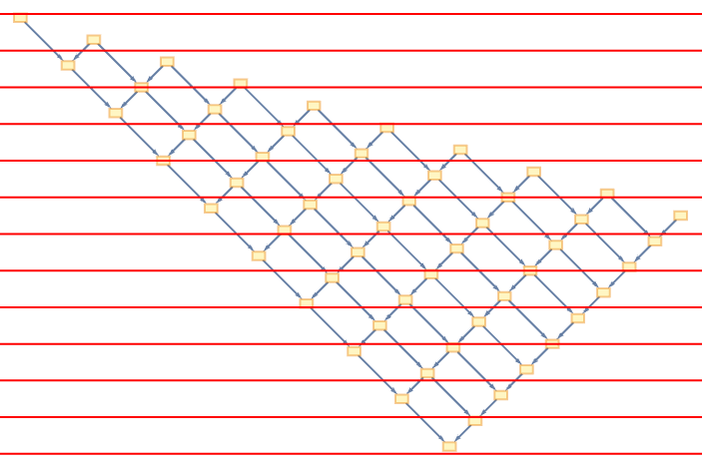
But this is precisely the usual Lorentz transformation of special relativity. And time dilation is then, for example, associated with the fact that to reach what corresponds to an event at slice t in the original foliation, one now has to go through a sequence of events that is longer by a factor of ![]() .
.
Normally one would argue for these results on the basis of principles supplied by special relativity. But the crucial point here is that in our models the results can be derived purely from the behavior of the models, without introducing additional principles.
Imagine simply using the transformed causal graph to determine the order of updating events in the underlying substitution system:

If we look vertically down the picture we see a different sequence of states of the system. But the crucial point is that the final outcome of the evolution is exactly the same as it was with the original foliation. In some sense the “physics” is the same, independent of the reference frame. And this is the essence of relativistic invariance (and here we immediately see some of its consequences, like time dilation).
But in the context of the string substitution system, we can now see its origin of the invariance. It is the fact that the underlying rule we have used is causal invariant, so that regardless of the specific order in which updating events occur, the same causal graph is obtained, with the same final output.
In our actual models based on infinitely evolving hypergraphs, the details are considerably more complicated. But the principles are exactly the same: if the underlying rule has causal invariance, its limiting behavior will show relativistic invariance, and (so long as it has limiting geometry corresponding to flat d-dimensional space) all the usual phenomena of special relativity.
(Note that the concept of a finite speed of light, leading effectively to locality in the causal graph, is related to the fact that the underlying rules involve rewriting hypergraphs only of bounded size.)
 download pdf
download pdf  ARXIV
ARXIV peer review
peer review