The examples we have discussed so far all contain only relations involving two elements, which can readily be represented as ordinary directed graphs. But in the class of models we consider, it is also possible to have relations involving other numbers of elements, say three.
As an example, consider:
which consists of two ternary relations. Such an object can be represented as a hypergraph consisting of two ternary hyperedges:
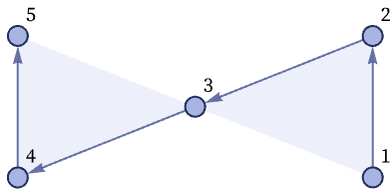
Because our relations are ordered, the hypergraph is directed, as indicated by the arrows around each hyperedge.
Note that hypergraphs can contain full or partial self-loops, as in the example of
which can be drawn as:
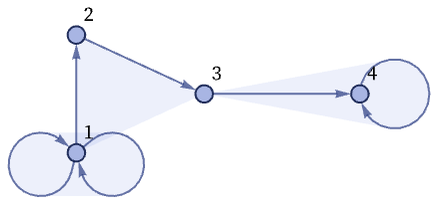
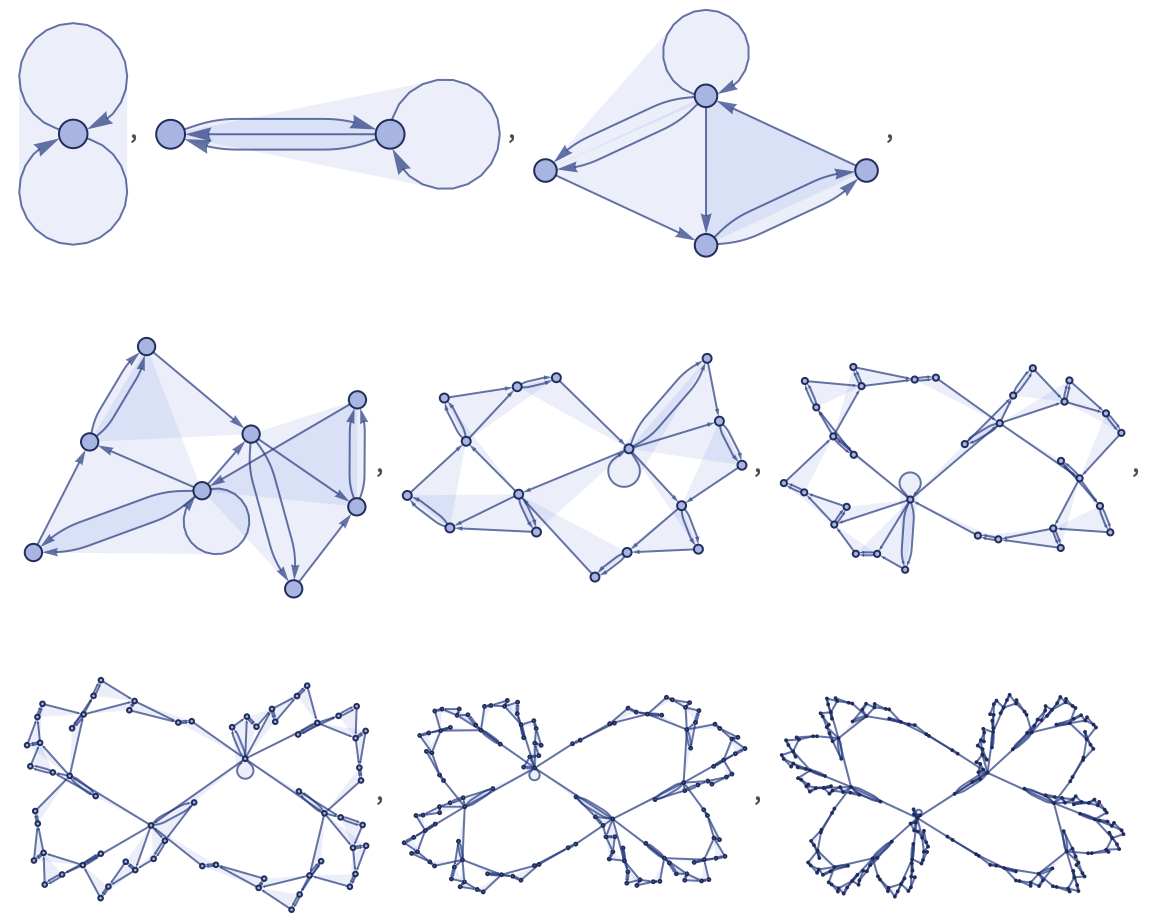
Rules can involve k-ary relations. Here is an example with ternary relations:
This rule can be represented as:
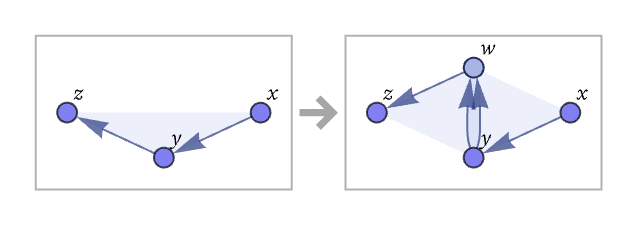
Starting from a single ternary self-loop, here are the first few steps obtained with this rule:
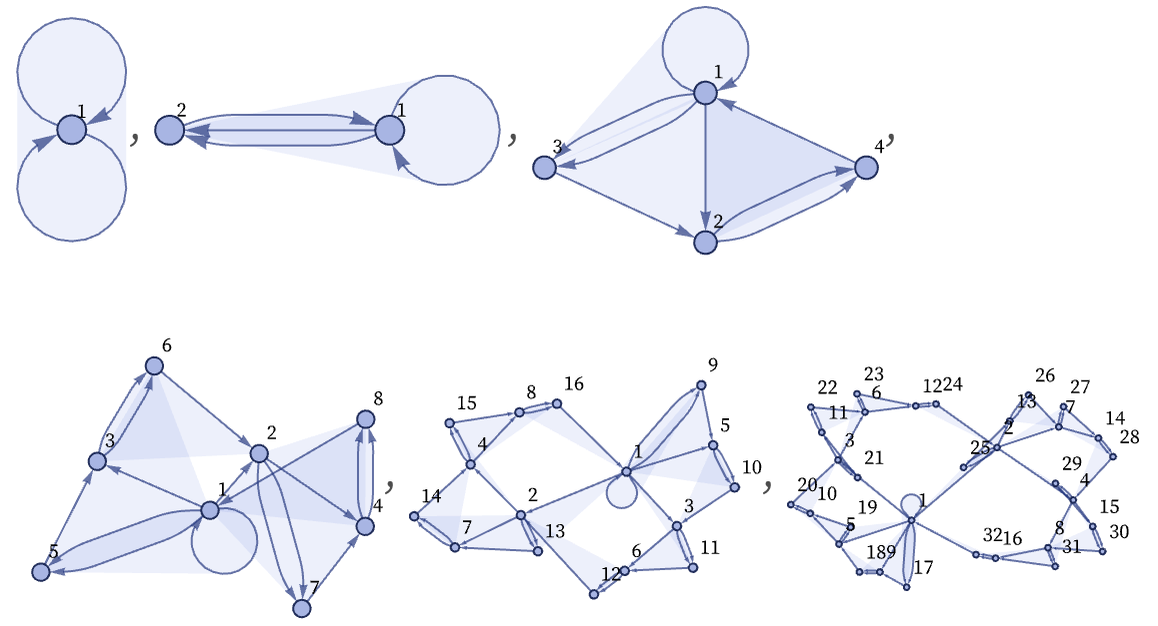
Continuing with this rule gives the following result:
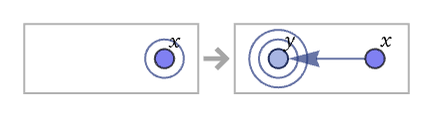
It is worth noting that in addition to having relations involving 3 or more elements, it is also possible to have relations with just one element. Here is an example of a rule involving unary relations:
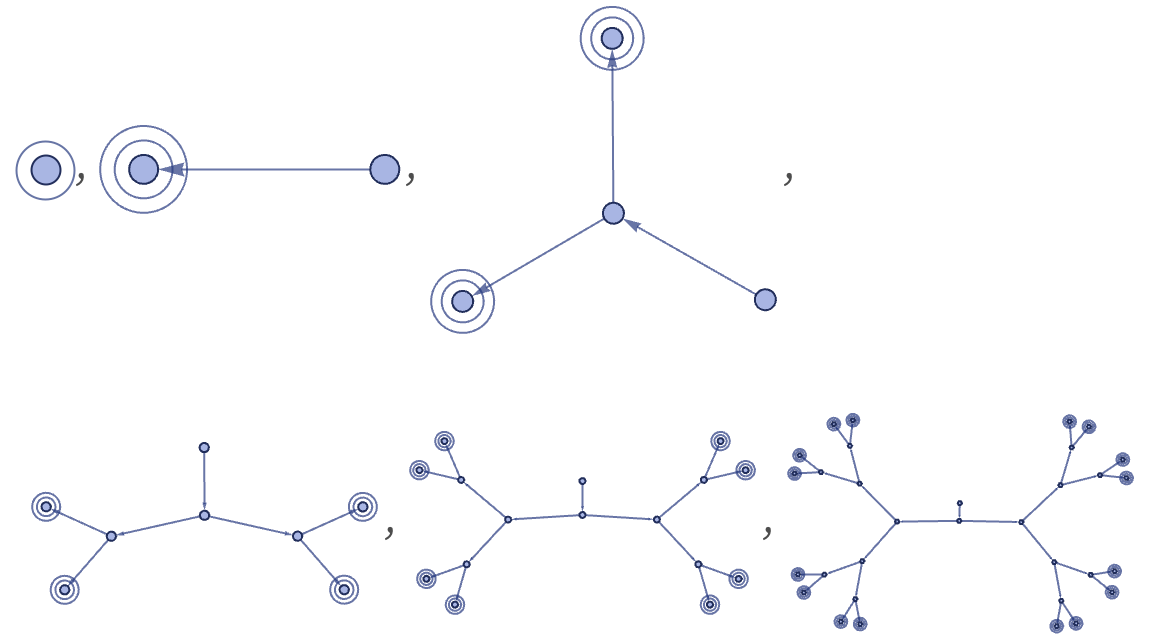
Starting from a unary self-loop, this rule leads to a binary tree with double-unary self-loops as leaves:
 download pdf
download pdf  ARXIV
ARXIV peer review
peer review