The phenomenon of intrinsic randomness generation is an important and ubiquitous feature of computational systems [1:7.5][39]—the rule 30 cellular automaton [1:2.1] being a quintessential example. In our models the phenomenon definitely often occurs, but two issues make it slightly more difficult to identify.
First, there is considerable arbitrariness in the way we choose to present or visualize graphs or hypergraphs—so it is more difficult to tell whether apparent randomness we see is a genuine feature of our system, or just a reflection of some aspect of our presentation or visualization method.
And second, there may be many possible choices of updating orders, and the specific results we get may depend on the order we choose. Later we will discuss the phenomenon of causal invariance, and we will see that there are causal graphs that can be independent of updating order. But for now, we can consider our updating process to just be another deterministic procedure added to the rules of our system, and we can ask about apparent randomness for this combined system.
And to avoid the arbitrariness of different graph or hypergraph presentations, we can look at graph or hypergraph invariants, which are the same for all isomorphic graphs or hypergraphs, independent of their presentation or visualization.
The most obvious invariants to start with are the total numbers of elements and relations (nodes and edges) in the system. For rules that involve only a single relation on the left-hand side, it is inevitable that these numbers must be determined by a linear recurrence (cf. [1:p890]). (For 1k nk rules, up to a k-term linear recurrence may be involved.)
For rules that involve more than one relation more complicated behavior is common. Consider for example the rule:
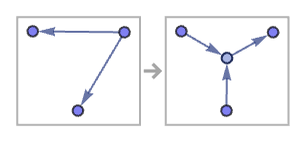
The number of relations generated over the first 50 steps (using our standard updating order) is:
Taking third differences yields:
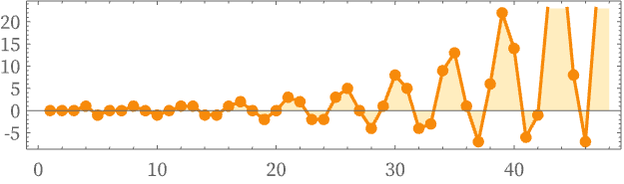
One can consider many other invariants, including counts of in and out degrees of elements, and counts of cycles. In general, one can construct invariant “fingerprints” of hypergraphs—and the typical observation is that for rules whose behavior seems complex, almost all of these will exhibit extensive apparent randomness.
 download pdf
download pdf  ARXIV
ARXIV peer review
peer review