A Class of Models with the Potential to Represent Fundamental Physics
  1. Introduction
  2. Basic Form of Models
  3. Typical Behaviors
  4. Limiting Behavior and Emergent Geometry
  5. The Updating Process for String Substitution Systems
  6. The Updating Process in Our Models
  7. Equivalence and Computation in Our Models
  8. Potential Relation to Physics
  9. Additional Material
  10. References
  11. Index
Download PDf download pdf
ARXIV ARXIV
peer-review peer review
technical introduction Typical Behaviors

3.9 Binary Rules with Signatures Beyond 2242

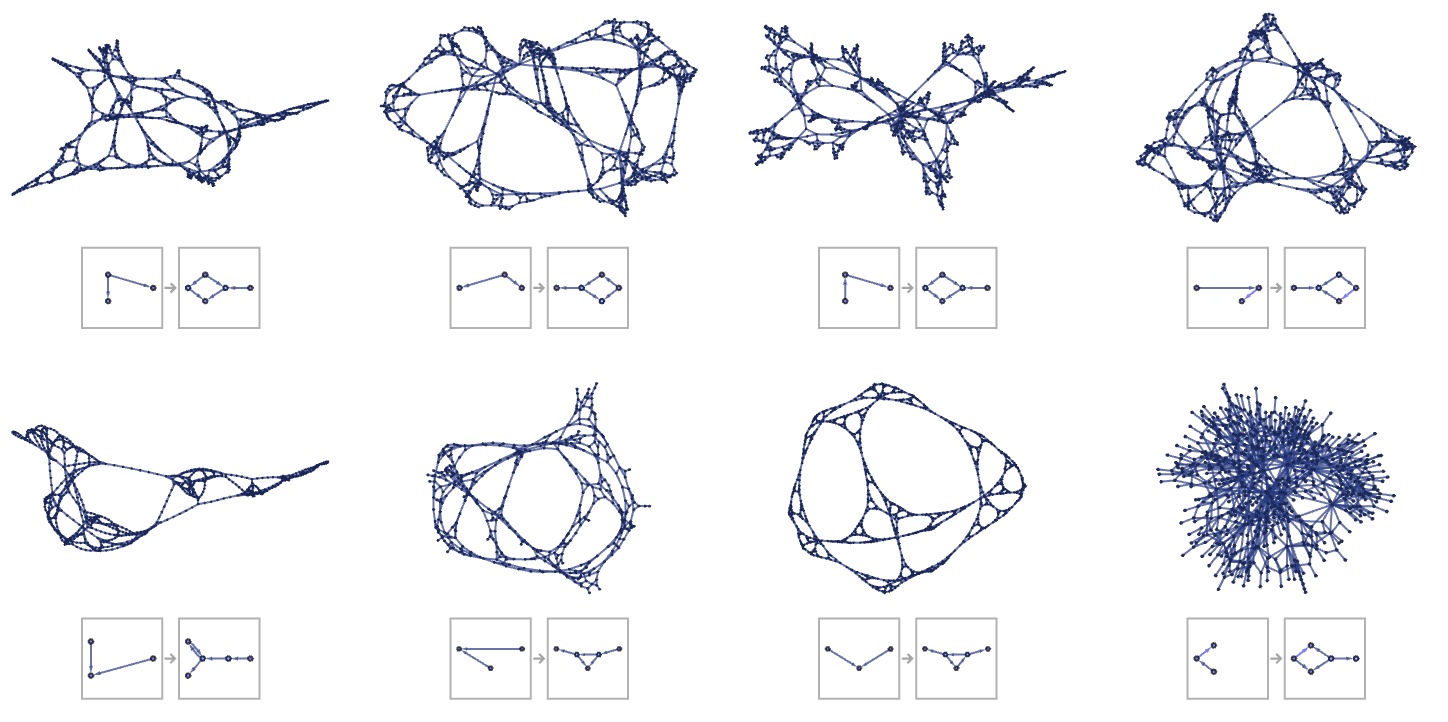
Going from signature 22 32 to signature 22 42 brought us the phenomenon of globular structures. Going to signature 22 52 and beyond does not seem to bring us any similarly widespread significant new form of behavior. The fraction of rules that yield connected results decreases, but among connected results, similar fractions of globular structures are seen, with examples from 22 52 including:

GraphicsGrid[ Partition[ ParallelMap[ Labeled[ResourceFunction["WolframModelPlot"][ ResourceFunction["WolframModel"][#[[1]], #[[2]], #[[3]], "FinalState"], ImageSize -> 1.1 {150, 100}], RulePlot[ResourceFunction["WolframModel"][#[[1]]], ImageSize -> Tiny, "RulePartsAspectRatio" -> 1]] &, {{{{1, 2}, {1, 3}} -> {{1, 4}, {1, 5}, {2, 4}, {4, 3}, {5, 3}}, {{0, 0}, {0, 0}}, 11}, {{{1, 2}, {1, 3}} -> {{2, 1}, {2, 4}, {1, 5}, {5, 4}, {5, 3}}, {{0, 0}, {0, 0}}, 8}, {{{1, 2}, {2, 3}} -> {{2, 4}, {2, 5}, {4, 1}, {5, 1}, {3, 4}}, {{0, 0}, {0, 0}}, 8}, {{{1, 2}, {2, 3}} -> {{4, 2}, {4, 5}, {2, 3}, {3, 5}, {1, 5}}, {{0, 0}, {0, 0}}, 10}, {{{1, 2}, {3, 2}} -> {{4, 1}, {1, 4}, {4, 2}, {5, 4}, {3, 5}}, {{0, 0}, {0, 0}}, 9}, {{{1, 2}, {3, 2}} -> {{4, 5}, {4, 1}, {5, 1}, {5, 2}, {3, 4}}, {{0, 0}, {0, 0}}, 11}, {{{1, 2}, {3, 2}} -> {{4, 5}, {5, 2}, {2, 4}, {4, 1}, {5, 3}}, {{0, 0}, {0, 0}}, 10}, {{{1, 2}, {2, 3}} -> {{4, 1}, {4, 3}, {2, 1}, {2, 3}, {4, 5}}, {{0, 0}, {0, 0}}, 9}}], UpTo[4]], ImageSize -> Full, Alignment -> Bottom]

The last rule shown here has a feature that is seen in a few 22 42 rules, but is more prominent in 22 52 rules: the presence of many “dangling ends” that at least visually obscure the structure. To see the structure better, one can take the evolution of this rule

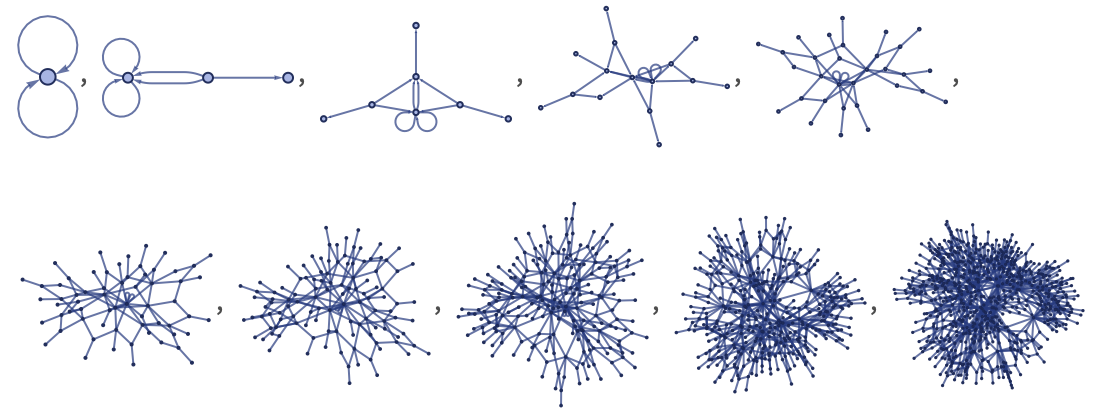
ResourceFunction["WolframModelPlot"][#, "MaxImageSize" -> 100] & /@ ResourceFunction[ "WolframModel"][{{1, 2}, {2, 3}} -> {{4, 1}, {4, 3}, {2, 1}, {2, 3}, {4, 5}}, {{0, 0}, {0, 0}}, 9, "StatesList"]

and effectively just “edit” the graphs obtained at each step, removing all dangling ends:

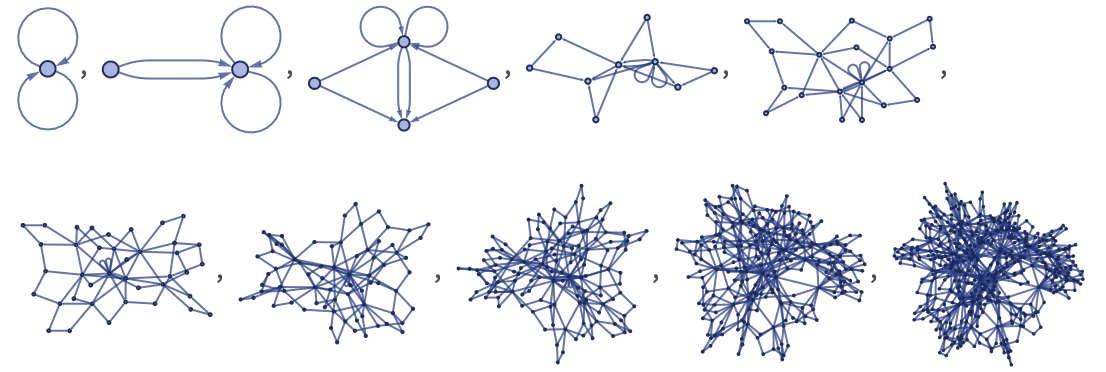
RemoveDanglingEndsU[graph_] := VertexDelete[graph, Pick[VertexList[graph], # < 2 & /@ VertexOutDegree[UndirectedGraph[graph]]]] ResourceFunction["WolframModelPlot"][#, "MaxImageSize" -> 100] & /@ Apply[List, EdgeList /@ RemoveDanglingEndsU /@ Graph /@ Apply[Rule, ResourceFunction[ "WolframModel"][{{1, 2}, {2, 3}} -> {{4, 1}, {4, 3}, {2, 1}, {2, 3}, {4, 5}}, {{0, 0}, {0, 0}}, 9, "StatesList"], {2}], {2}]

In addition to increasing the number of relations on the right-hand side of the rule, one can also increase the number on the left. For example, one can consider 32 42 rules. These much more often lead to termination than 22 … rules, and appear to produce results generally similar to 22 32 rules.

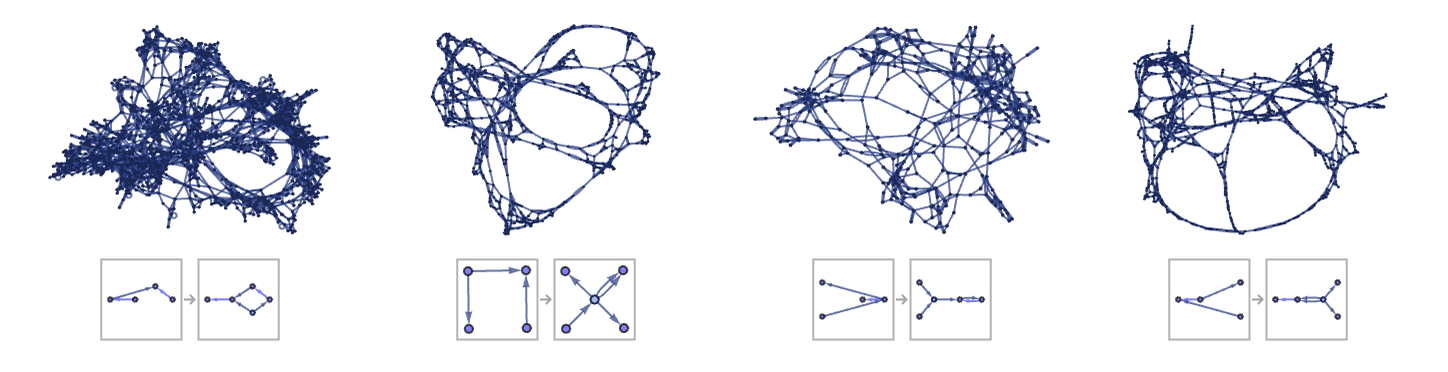
32 52 rules also produce globular structures, though more rarely than 22 42 rules, and with slower growth. A few examples are:

GraphicsRow[ ParallelMap[ Labeled[ResourceFunction["WolframModelPlot"][ ResourceFunction["WolframModel"][#[[1]], #[[2]], #[[3]], "FinalState"], ImageSize -> 1.1 {150, 100}], RulePlot[ResourceFunction["WolframModel"][#[[1]]], "RulePartsAspectRatio" -> 1, ImageSize -> Tiny]] &, {{{{1, 2}, {2, 3}, {4, 3}} -> {{5, 4}, {5, 1}, {4, 3}, {3, 1}, {1, 2}}, {{0, 0}, {0, 0}, {0, 0}}, 16}, {{{1, 2}, {1, 3}, {4, 2}} -> {{5, 2}, {5, 2}, {5, 1}, {5, 4}, {3, 5}}, {{0, 0}, {0, 0}, {0, 0}}, 16}, {{{1, 2}, {1, 3}, {4, 1}} -> {{2, 1}, {1, 2}, {5, 2}, {3, 5}, {4, 5}}, {{0, 0}, {0, 0}, {0, 0}}, 16}, {{{1, 2}, {1, 3}, {4, 2}} -> {{5, 1}, {5, 1}, {5, 3}, {5, 4}, {1, 2}}, {{0, 0}, {0, 0}, {0, 0}}, 16}}], ImageSize -> Full]
  • Download Notebook
  • Open in Wolfram Cloud
  • Discuss This Page