A Class of Models with the Potential to Represent Fundamental Physics
  1. Introduction
  2. Basic Form of Models
  3. Typical Behaviors
  4. Limiting Behavior and Emergent Geometry
  5. The Updating Process for String Substitution Systems
  6. The Updating Process in Our Models
  7. Equivalence and Computation in Our Models
  8. Potential Relation to Physics
  9. Additional Material
  10. References
  11. Index
Download PDf download pdf
ARXIV ARXIV
peer-review peer review
technical introduction Typical Behaviors

3.11 Rules Involving More Ternary Relations

There are about 9 billion inequivalent left-connected 23 43 rules. About 20% lead to connected results, and of these about half show continued growth. Here is a random sampling of the behavior of such rules:

The fraction of complex behavior appears to be no higher than for 23 33 rules, and no obvious major new phenomena are seen. Much like in systems such as cellular automata (and as suggested by the Principle of Computational Equivalence [1:12]), above some low threshold, adding complexity to the rules does not appear to add complexity to the typical behavior produced.

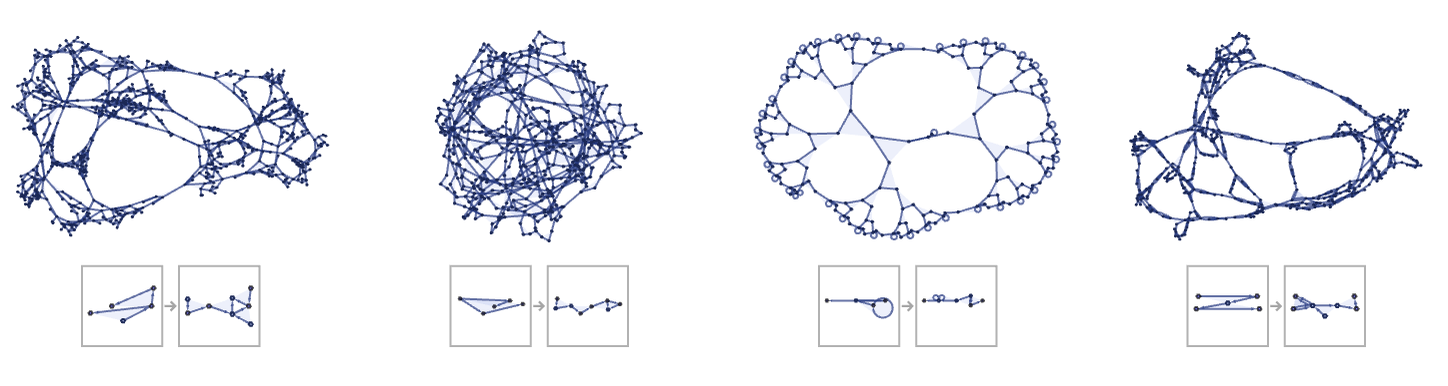
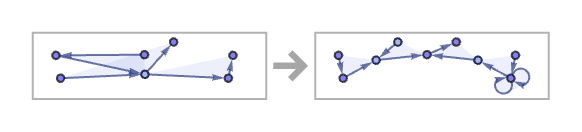
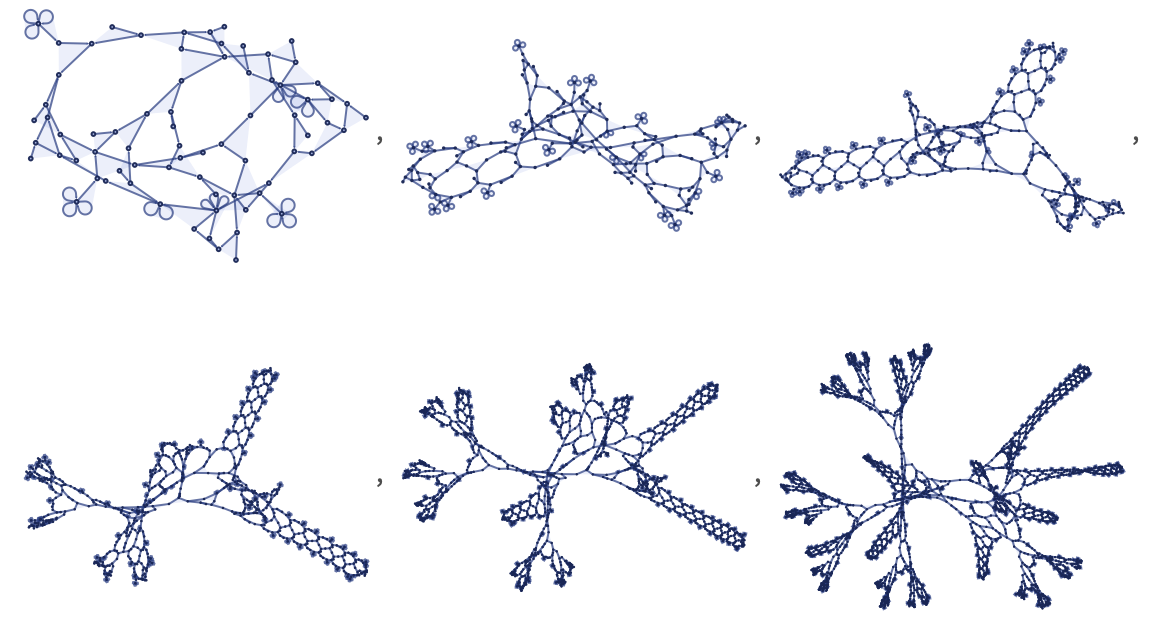
The trend continues with 33 43 rules, with one notable feature here being an increased propensity for rules to yield results that become disconnected, though only after many steps. The general difficulty of predicting long-term behavior is illustrated for example by the evolution of this 33 53 rule, sampled every 10 steps:

  • Download Notebook
  • Open in Wolfram Cloud
  • Discuss This Page