One of the surprising consequences of the potential application of our models to physics is their implications around deep relationships between relativity and quantum mechanics. These are particularly evident in thinking about the multiway causal graph. As a toy model, consider the graph:
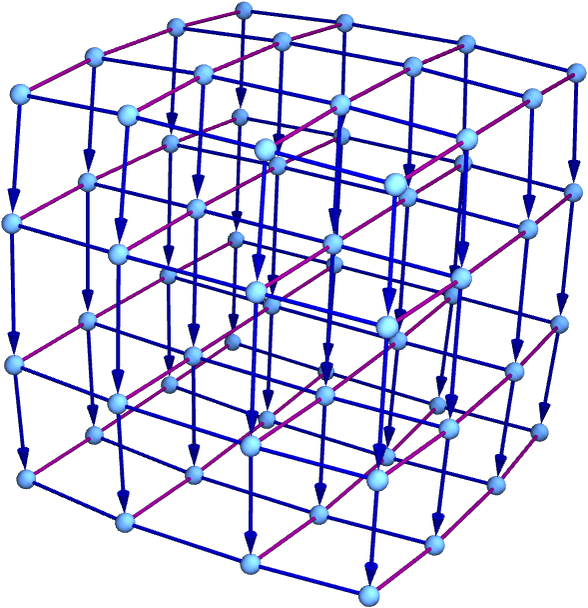
Timelike edges go down, but then in each slice there are spacelike and branchlike edges. A more realistic example of the very beginning of such a graph is:
The multiway causal graph in a sense captures in one graph both relativity and quantum mechanics. Time is involved in both of them, and in our models it is an essentially computational concept, involving progressive application of the underlying rules of the system. But then relativity is associated with the structure formed by spacelike and timelike edges, while quantum mechanics is primarily associated with the structure formed by branchlike and timelike edges.
The spacelike direction corresponds to ordinary physical space; the branchlike direction is effectively the space of quantum states. Distance in the spacelike direction is ordinary spacetime distance. Distance in the branchlike direction reflects the level of quantum entanglement between states. When we form foliations in time, spacelike hypersurfaces represent in a sense the instantaneous configuration of space, while branchlike hypersurfaces represent the instantaneous entanglements between quantum states.
It should be emphasized that (unlike in the idealization of our first picture above) the detailed structure of the spacelike+timelike component of the multiway causal graph will in practice be very different from that of the branchlike+timelike one. The spacelike+timelike component is expected to limit to something like a finite-dimensional manifold, reflecting the characteristics of physical spacetime. The branchlike+timelike one potentially limits to an infinite dimensional space (that is perhaps a projective Hilbert space), reflecting the characteristics of the space of quantum states. But despite these substantial geometrical differences, one can expect many structural aspects and consequences to be basically the same.
We are used to the idea of motion in space. In the context of our models—and of the multiway causal graph—motion in space in effect corresponds to progressively sampling more spacelike edges in the graph. But now we can see a quantum analog: we can also have motion in the branchlike direction, in which, in effect, we progressively sample more branchlike edges, reaching more quantum states. Velocity in space is thus the analog of the rate at which additional states are sampled (and thus entangled).
In relativity there is a fairly well-developed notion of an idealized observer. The observer is typically represented by some some causal foliation of spacetime—like an inertial reference frame that moves without forces acting on it. One can also define an observer in quantum mechanics, and in the context of our models it makes sense—as we have done above—to parametrize the observer in terms of a quantum observation frame that consists not of a sequence of spacelike hypersurfaces, but instead of a series of branchlike ones.
A quantum observation frame in a sense defines a plan for how an observer will sample possible quantum states—and the analog of an inertial frame in spacetime is presumably a quantum observation frame that corresponds to a fixed plan that cannot be affected by anything outside. And in general, the analog in quantum mechanics of a world line in relativity is presumably a measurement plan.
In special relativity a key idea is to think about comparing the perceptions of observers in different inertial frames. But in the context of our models we can now do the exact same thing for quantum observers. And the analog of relativistic invariance then becomes a statement of perception or measurement invariance: that in the end different quantum observers (despite the branching of states) in a sense perceive the same things to happen, or, in other words, that there is at some level an objective reality even in quantum mechanics.
Our analogy between relativity and quantum mechanics suggests asking about quantum analogs of standard relativistic phenomena. One example is relativistic time dilation, in which, in effect, sampling spacelike edges faster reduces the rate of traversing timelike edges. The analog in quantum mechanics is presumably the quantum Zeno effect [126][127], in which more rapid measurement—corresponding to faster sampling of branchlike edges—slows the time evolution of a quantum system.
A key concept in relativity is the light cone, which characterizes the maximum rate at which causal effects spread in spacelike directions. In our models, spacetime causal edges in effect define elementary light cones, which are then knitted together by the structure of the (spacetime) causal graph. But now in our models there is a direct analog for quantum mechanics, visible in the full multiway causal graph.
In the multiway causal graph, every event effectively has a cone of causal influence. Some of that influence may be in spacelike directions (corresponding to ordinary relativistic light cone effects), but some of it may be in branchlike directions. And indeed, whenever there are branches in the multiway graph, these correspond to branchlike edges in the multiway causal graph.
So what this means is that in addition to a light cone of effects in spacetime, there is also what we may call an entanglement cone, which defines the region affected in branchial space by some event. In the light cone case, the spacelike extent of the light cone is set by the speed of light (c). In the entanglement cone case (as we will discuss below) the branchlike extent of the entanglement cone is essentially set by ℏ.
As we have mentioned, the definition of time is shared between spacelike and branchlike components of the multiway causal graph. Another shared concept appears to be energy (or in general, energy-momentum, or action). Time is effectively defined by displacement in the timelike direction; energy appears to be defined by the flux of causal edges in the timelike direction. In the relativistic setting, energy can be thought of as flux of causal edges through spacelike hypersurfaces; in the quantum mechanical setting, it can be thought of as a flux of causal edges through branchlike hypersurfaces.
An important feature of the spacetime causal graph is that it can potentially describe curved space, and reproduce general relativity. And here again we can now see that in our models there are analogs in quantum mechanics. One issue, though, is that whereas ordinary space is—at least on a large scale—finite-dimensional, comparatively flat, and well modeled by a simple Lorentzian manifold, branchial space is much more complicated, probably in the limit infinite–dimensional, and not at all flat.
At a mathematical level, we are in quantum mechanics used to forming commutators of operators, and in many cases finding that they do not commute, with their “deviation” being measured by ℏ. In general relativity, one can also form commutators, and indeed the Riemann tensor for measuring curvature is precisely the result of computing the commutator of two covariant derivatives. And perhaps even more analogously the Ricci scalar curvature gives the angle deficit for transport around a loop in spacetime.
In our context, therefore, the non-flatness of space is directly analogous to a core phenomenon of quantum mechanics: the non-commuting of operators.
In the general relativity case, we are used to thinking about the propagation of bundles of geodesics in spacetime, and the fact that the Ricci scalar curvature determines the local cross-section of the bundle. Now we can also consider the more general propagation of bundles of geodesics in the multiway causal graph. But when we look along branchlike directions, the limiting space we see tends to be highly connected, and effectively of high negative curvature. And what this means is that a bundle of geodesics can be expected to spread out rapidly in branchlike directions.
But this has an immediate interpretation in quantum mechanics: it is the phenomenon of decoherence, whereby quantum effects get spread (and entangled) across large numbers of quantum degrees of freedom.
In relativity, the speed of light c sets a maximum speed for the propagation of effects in space. In quantum mechanics, our entanglement cones in essence also set a maximum speed for the propagation of effects in branchial space. In special relativity, there is then a maximum speed defined for any observer—or, in other words, a maximum speed for motion. In quantum mechanics, we can now expect that there will also be a maximum speed for entanglement, or for measurement: it is not possible to set up a quantum observation frame that achieves a higher speed while still respecting the causal relations in the multiway causal graph. We will call this maximum speed ζ, and in 8.20 we will discuss its possible magnitude.
One may ask to what extent the correspondences between relativity and quantum mechanics that we have been discussing rely on our models. In principle, for example, one could imagine a kind of “multicausal continuum” that is a mathematical structure (conceivably related to twistor spaces [128]) corresponding to a continuum limit of our multiway causal graph. But while there are challenges in understanding the limits associated with our models, this seems likely to be even more difficult to construct and handle—and has the great disadvantage that it cannot be connected to explicit models that are readily amenable, for example, to enumeration.
 download pdf
download pdf  ARXIV
ARXIV peer review
peer review