The grids and surfaces that we saw above were all produced by rules that end up executing a laborious “knitting” process in which they add just a single relation at each step. But it is also possible to generate recognizable geometric forms more quickly—in effect by a process of repeated subdivision.
Consider the 2312 4342 rule:
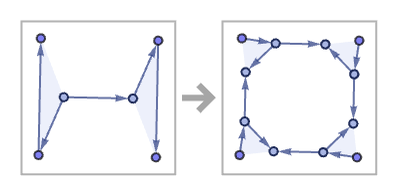
At each step, this rule doubles the number of relations—and quickly produces a structure with a definite emergent geometrical form:
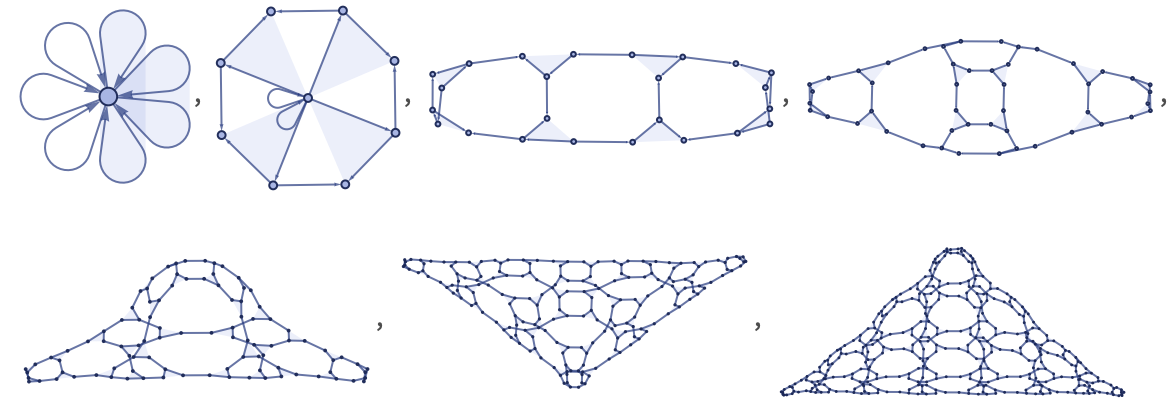
After 10 steps the rule has generated 2560 relations, in the following structure:
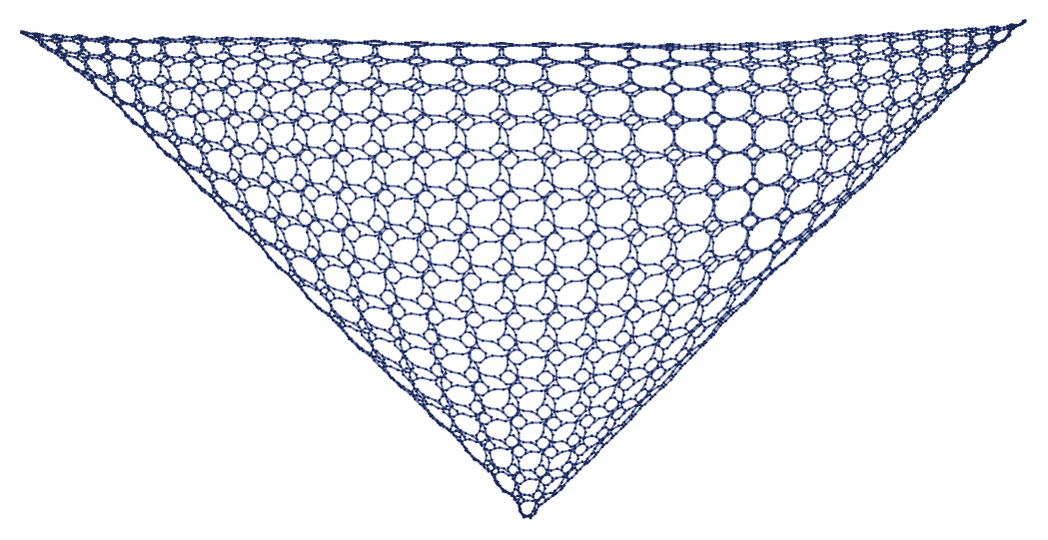
Visualized in 3D, this becomes:

Once again, this corresponds to a smooth surface, but with 3 cusps. The surface is defined not by a simple triangular grid, but instead by an octagon-square (“truncated square”) tiling—that in this case becomes twice as fine at every step.
Changing the initial conditions can give a somewhat different structure:
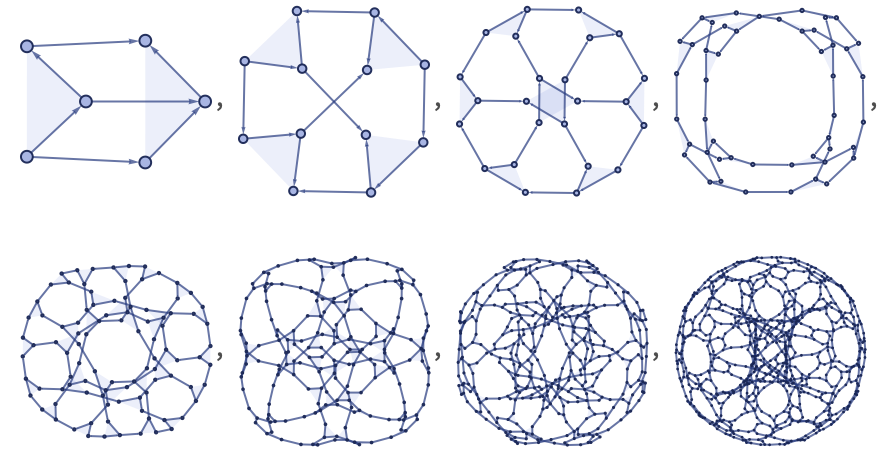
Visualized in 3D after 10 steps (and reconstructing less of the surface), this becomes:

 download pdf
download pdf  ARXIV
ARXIV peer review
peer review