Essentially all the rules we have considered so far have been set up to add relations. But with extended initial conditions, it makes sense also to consider rules that maintain a fixed number of relations.
Rules with signatures like 12 12 that depend only on one relation cannot give rise to nontrivial behavior. But rules with signature 22 22 (of which a total of 562 are inequivalent) already can.
Consider the rule:
Starting from a chain of 5 binary relations, this is the behavior of the rule:

Given that only a finite number of elements and relations are involved, the total number of possible states of the system is finite, so it is inevitable that the evolution of the system must eventually repeat. In the particular case shown here, the repetition period is only 3 steps. (Note that the detailed behavior—and the repetition period—can depend on the updating order used.)
In general, the total number of possible states of the system is given by the number of distinct hypergraphs of a certain size. One can then construct a state transition graph for these states under a rule. Here is the result for the rule above with the 32 distinct connected 32 hypergraphs (note that with this rule, the hypergraphs always remain connected):
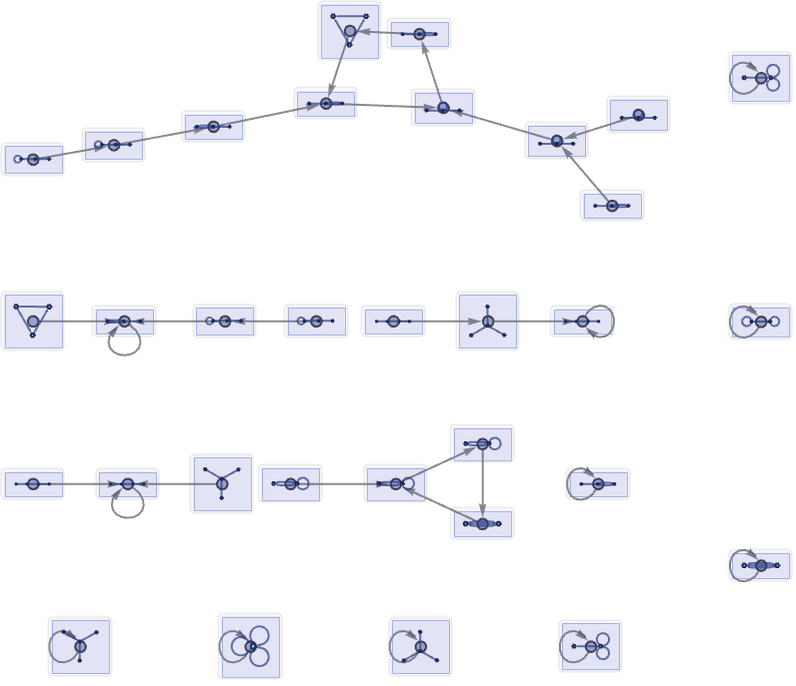
The result for all 928 52 hypergraphs is:
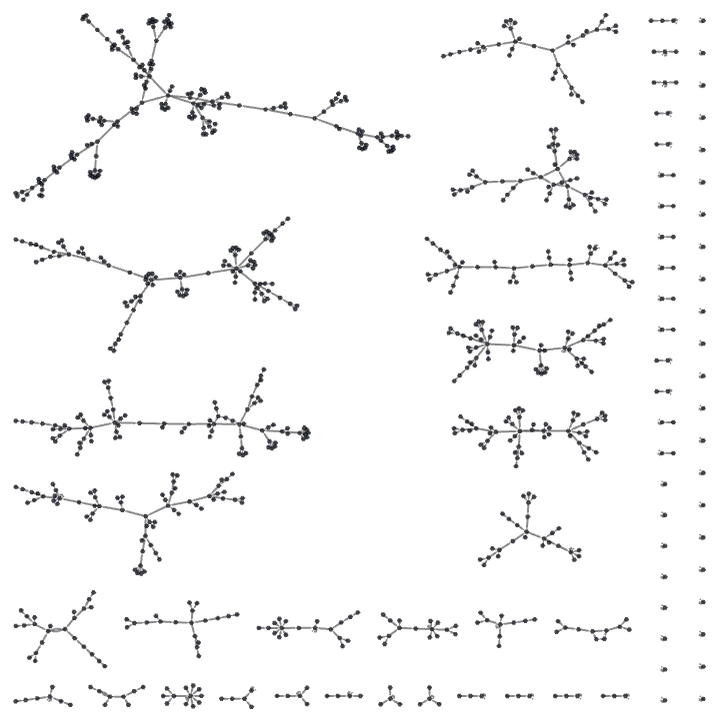
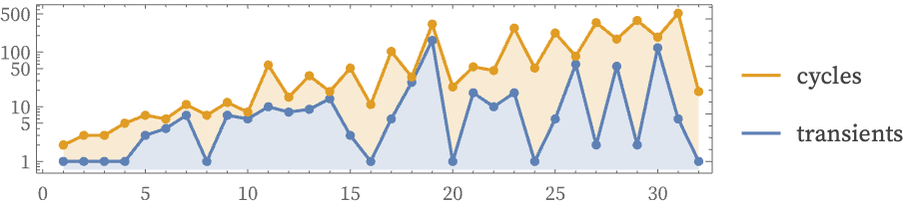
This graph contains trees corresponding to transients, leading into cycles. The maximum cycle length in this case is 5. But when the size of the system increases, the lengths of cycles can increase rapidly (cf. [1:6.4]). The length is bounded by the number of distinct nk hypergraphs, which grows faster than exponentially with n. The plot below shows the lengths of cycles and transients in the rule above for initial conditions consisting of progressively longer chains of relations:
 download pdf
download pdf  ARXIV
ARXIV peer review
peer review