A Class of Models with the Potential to Represent Fundamental Physics
  1. Introduction
  2. Basic Form of Models
  3. Typical Behaviors
  4. Limiting Behavior and Emergent Geometry
  5. The Updating Process for String Substitution Systems
  6. The Updating Process in Our Models
  7. Equivalence and Computation in Our Models
  8. Potential Relation to Physics
  9. Additional Material
  10. References
  11. Index
Download PDf download pdf
ARXIV ARXIV
peer-review peer review
technical introduction Typical Behaviors

3.4 Rules Depending on a Single Unary Relation

The very simplest possible rules are ones that transform a single unary relation, for example the 11 21 rule:

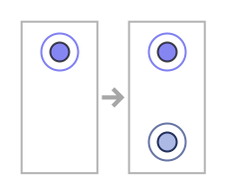
This rule generates a disconnected hypergraph, containing 2n disconnected unary hyperedges at step n:

To get less trivial behavior, one must introduce at least one binary relation. With the 11 1211 rule

one just gets a figure with progressively more binary-edge “arms” being added to the central unary hyperedge:

The rule

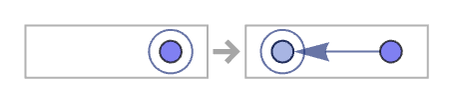
produces a growing linear structure, progressively “extruding” binary edges from the unary hyperedge:

With two unary relations and one binary relation (signature 11 1221) there are 16 possible rules; after 4 steps starting from a single unary relation, these give:

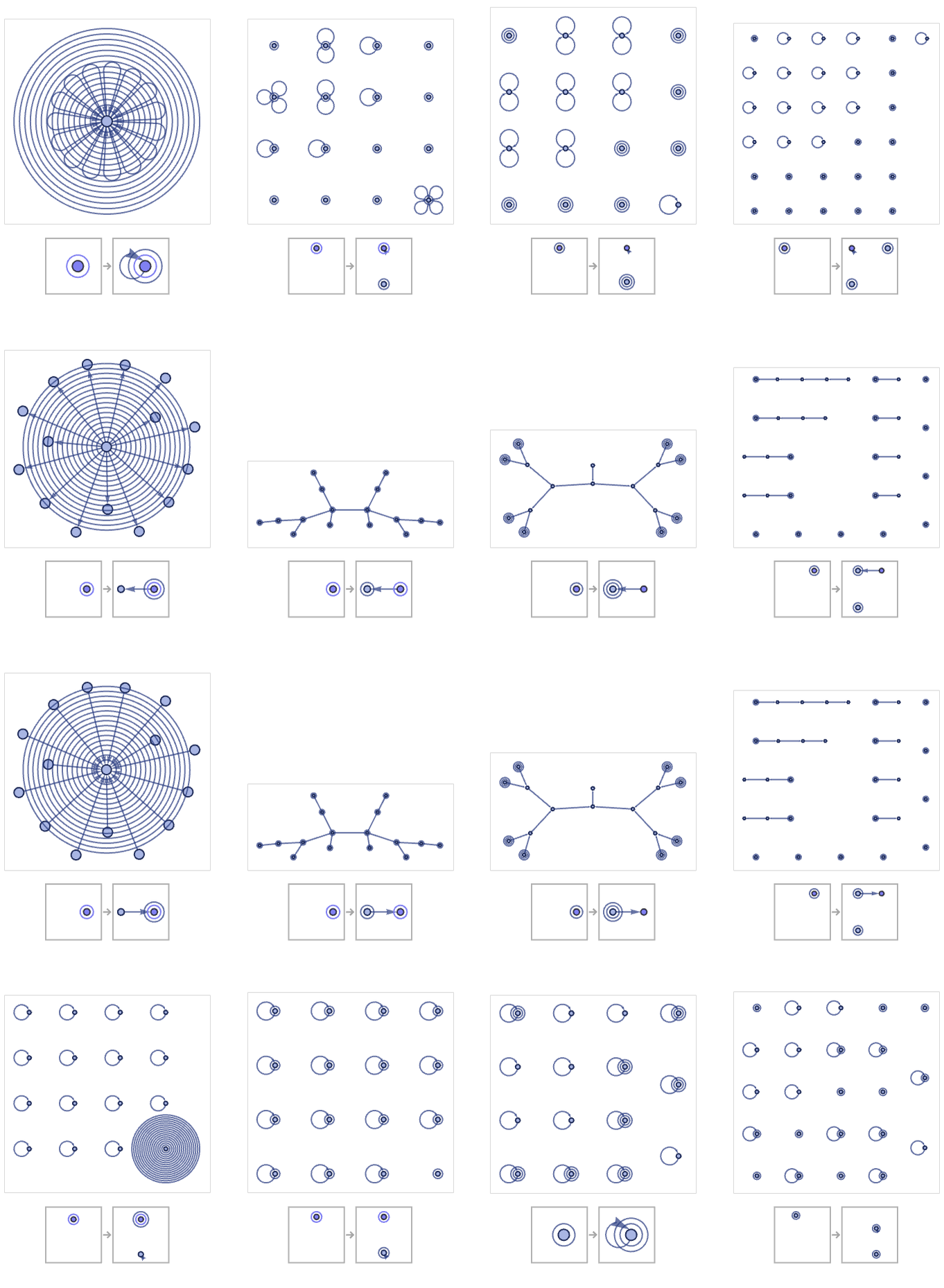
Many lead to disconnected hypergraphs; four lead to binary trees with structures we have already seen. ({{x}}→{{x,y},{x},{y}} is a 12 1221 rule that gives the same result as the very first 12 22 rule we saw.

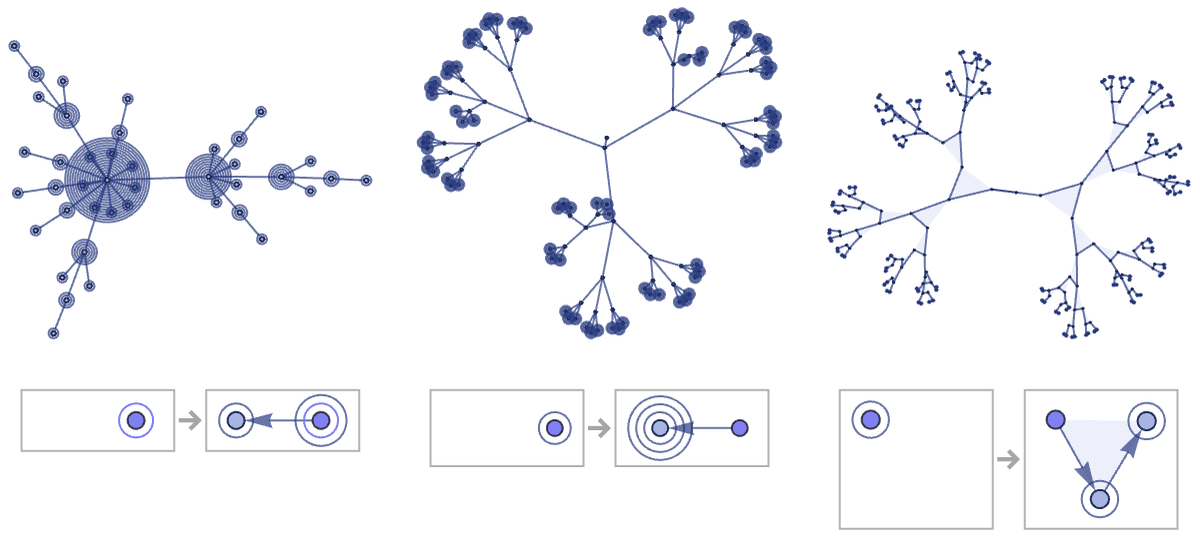
Rules for a single unary relation can never give structures more complex than trees, though the morphology of the trees can become slightly more elaborate:

  • Download Notebook
  • Open in Wolfram Cloud
  • Discuss This Page