A relation can contain two identical elements, as in {0,0}, corresponding to a self-loop in a graph. Starting our first rule from a single self-loop, the self-loop effectively just stays marking the original node:
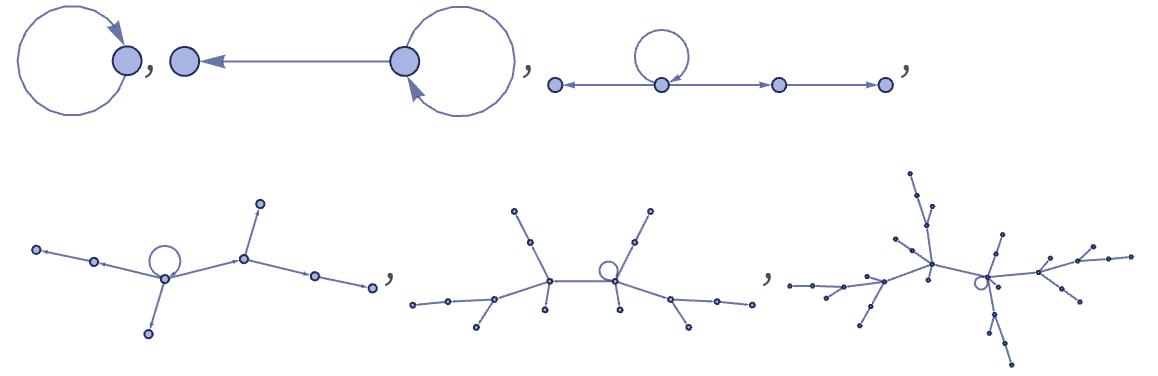
However, with for example the rule:
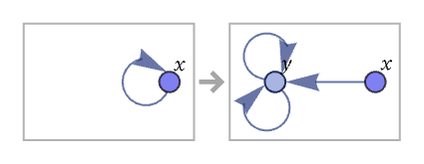
the self-loop effectively “takes over” the system, “inflating” to a 2n – gon:

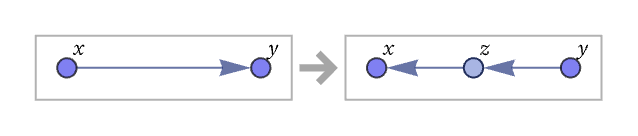
The rule can also contain self-loops. An example is
represented graphically as:
Starting from a single self-loop, this rule produces a simple binary tree:
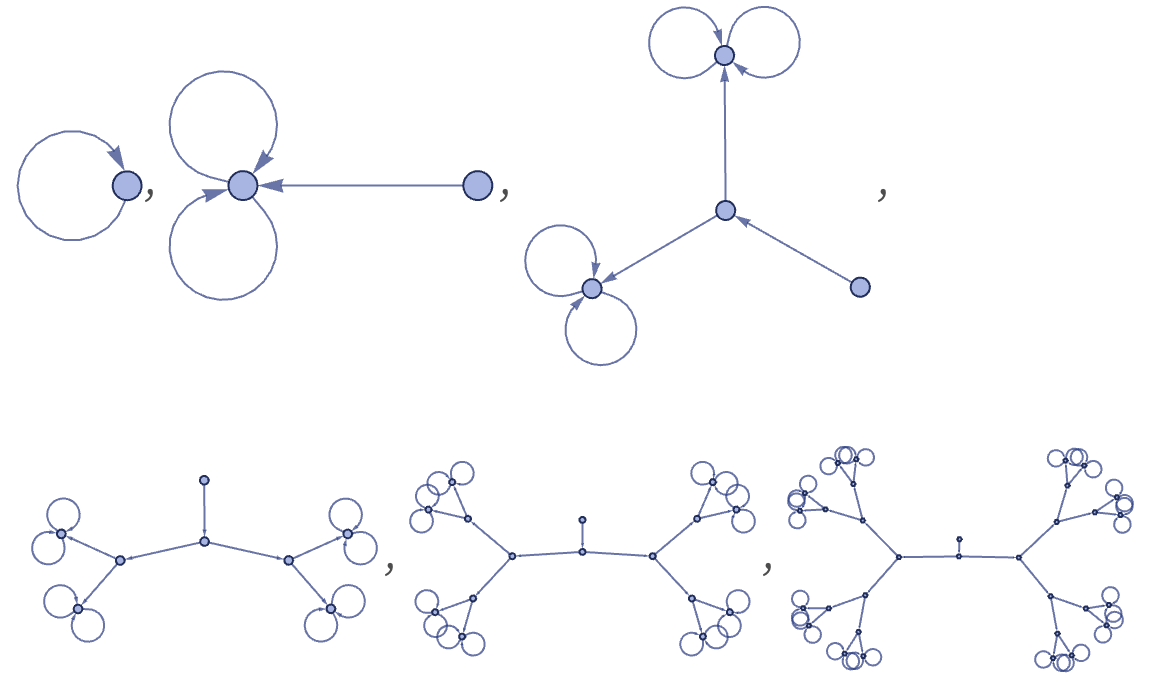
 download pdf
download pdf  ARXIV
ARXIV peer review
peer review