We have mostly restricted ourselves so far to cases where the results generated by a rule remain connected. But in fact if one looks at all possible rules the majority generate disconnected pieces, or at least can do so for certain initial conditions. Among the 73 rules with signature 12 22, only 33 generate connected results starting from initial condition {{0,0}} (and a further 10 terminate from this initial condition).
(Note that we are ignoring order in determining connectivity, so that, for example, the relation {1,2} is considered connected not only to {2,3} but also to {1,3}. Translating binary relations like these into directed edges in a graph, this means we are considering weak connectivity, or, equivalently, we are looking only at the undirected version of the graph.)
Most 12 22 rules that yield disconnected results essentially just produce exponentially more copies of the same structure:
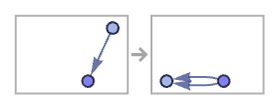

(Note that this rule is an example of one that yields disconnected results even though the rule itself is not disconnected.)
A few rules show slightly more complicated behavior. Examples are (wm575, wm879):
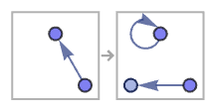



Both these rules still show exponentially increasing numbers of connected components. In the first case, at step t there are components of all sizes 1 through t, in exponentially decreasing numbers. In the second case, the size of the largest component is
or asymptotically ~ϕn (it follows the recurrence f[n]=2f[n–1]–f[n–3]).
Note that if one tracks only the largest component, one gets a sequence of results that could only be generated by a rule involving several separate transformations (in this case {{x,x}}→{{x,y},{x,x}} and {{x,y}}→{{x,x}}). In general, with a single transformation, the total number of relations must either always increase or always decrease. But if there are disconnected pieces, and one tracks, say, only the largest component, one can get a sequence of results that can both increase and decrease in size.
As an example, consider the rule:
Evolving this rule with our standard updating order gives:
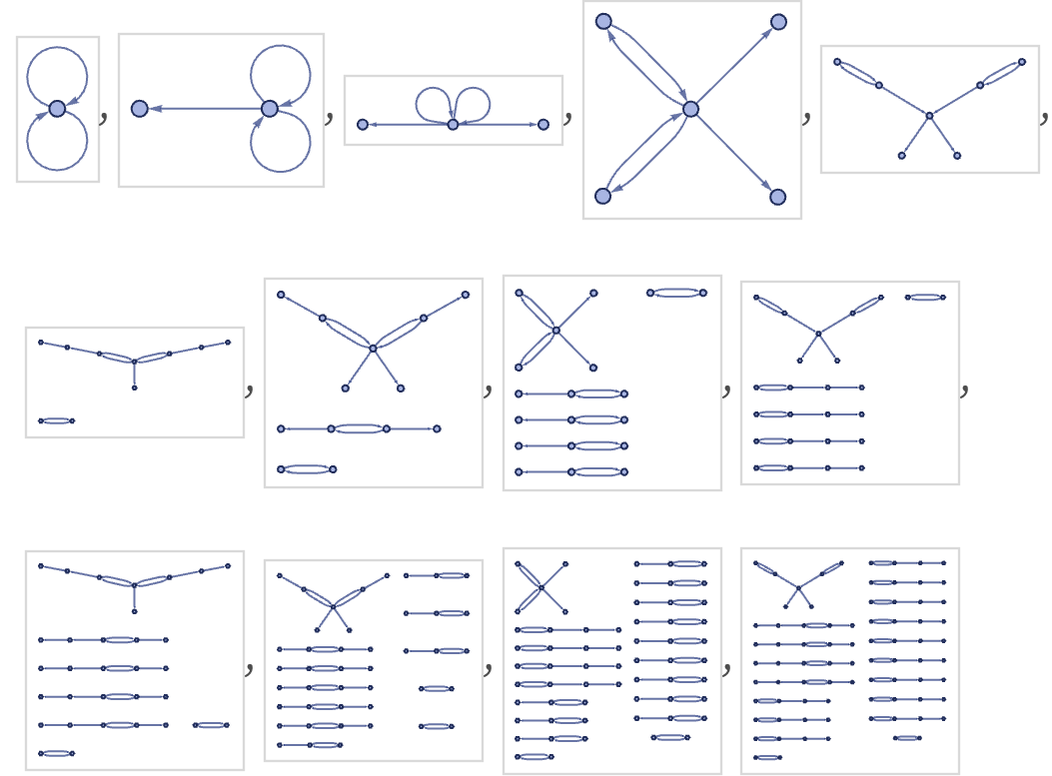
The total number of relations increases roughly exponentially. But tracing only the largest component, we see that it oscillates in size, eventually settling into the cycle 5,8,9,8:
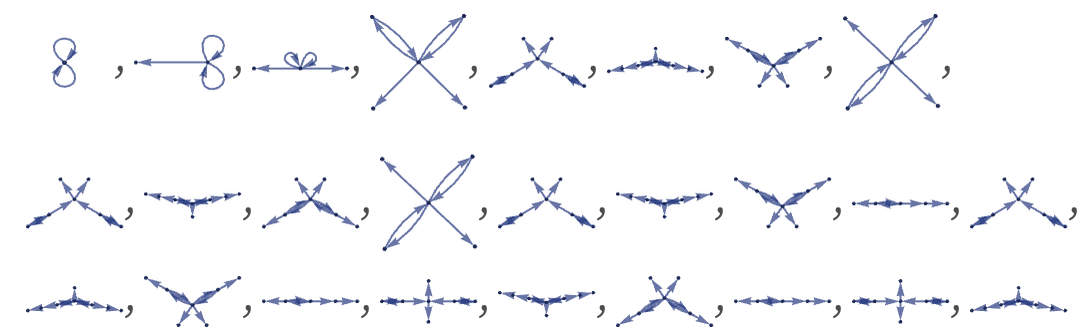
Note that this result is quite specific to the use of our standard updating order. A random updating order, for example, will typically give larger results for the largest component, and no cycle will normally be seen.
It is quite common to see rules that sometimes yield connected results, and sometimes do not. (In fact, proving that a given rule in a given case can never generate disconnected components can be arbitrarily difficult.) Sometimes there can be a large component with a complex structure, with small disconnected pieces occasionally getting “thrown off”. Consider for example the rule:
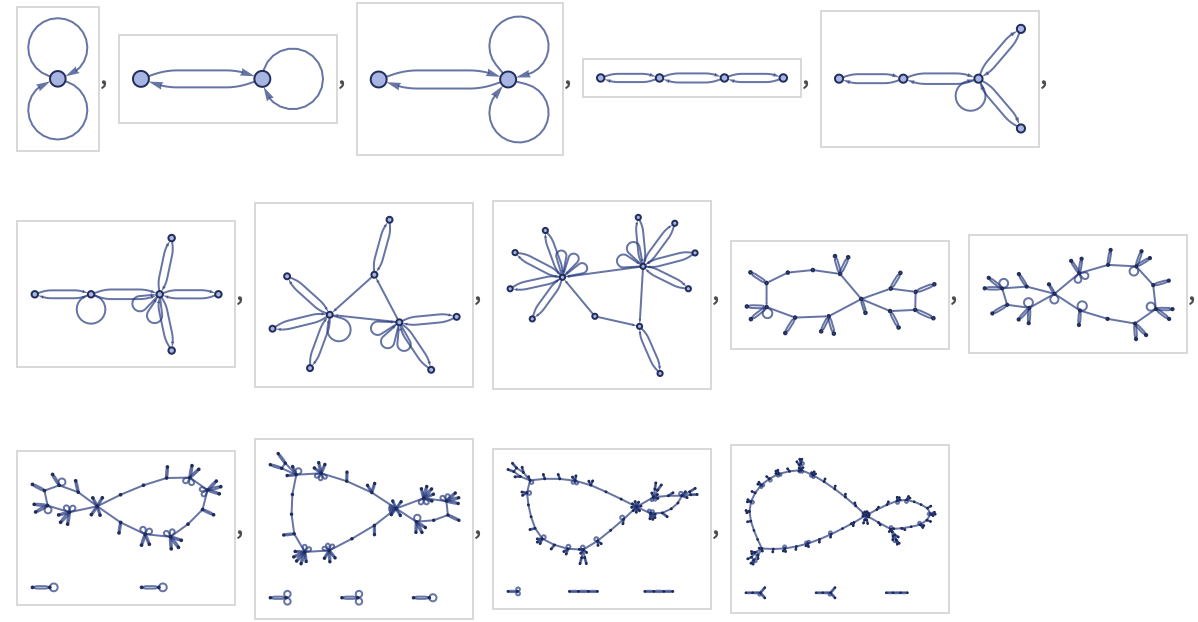
With the standard updating order, it remains connected for 10 steps, then suddenly starts throwing off small disconnected pieces.
As a more elaborate example, consider the rule:
This remains connected for 16 steps, then starts throwing off disconnected pieces:
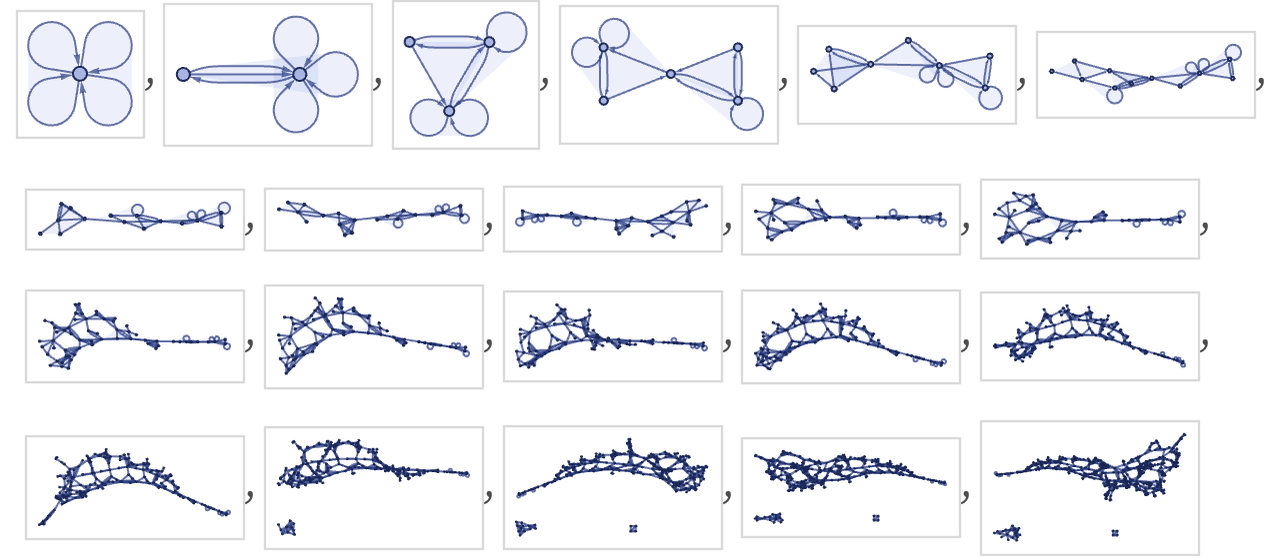
With a rule like this, once components become disconnected, they can in a sense never interact again; their evolutions become completely separate. The only way for disconnected components to interact is to have a rule which itself has a disconnected left-hand side.
For example, a rule like
will collect even completely disconnected unary relations, and connect pairs of them into binary relations:
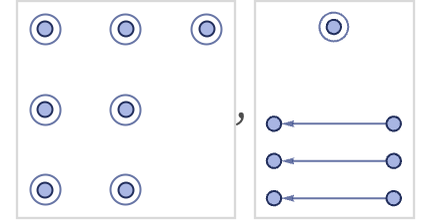
Connected unary relations (i.e. such as {1}, {1}, ...) can end up in the same component, but the result depends critically on the order in which updates are done:
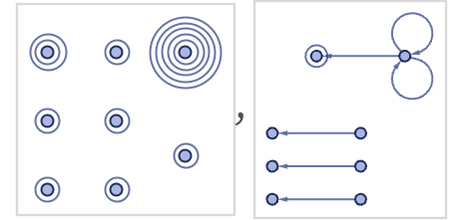
For now, we will not consider any further rules with disconnected left-hand sides—and the extreme nonlocality they represent.
 download pdf
download pdf  ARXIV
ARXIV peer review
peer review