8.19 Local Gauge Invariance

An important phenomenon discussed especially in the context of quantum field theories is local gauge invariance (e.g. [134]). In our models this phenomenon can potentially arise as a result of local symmetries associated with underlying rules (see 6.12). The basic idea is that these symmetries allow different local configurations of rule applications—that can be thought of as different local “gauge” coordinate systems.

But the collection of all such possible configurations appears in the multiway graph (and the multiway causal graph)—so that a local choice of gauge can then be represented by a particular foliation in the multiway graph. But causal invariance then implies the equivalence of foliations—and establishes local gauge invariance.

As a very simple example, consider the rule:

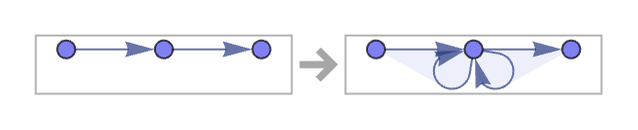
Starting from a square, this rule can be applied in two different ways:

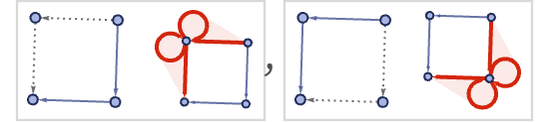
There is similar freedom if one applies the rule twice to a larger region:

In both cases one can think of the freedom to apply the rule in different ways as being like a symmetry, for example characterized by the list of possible permutations of input elements.

But now imagine taking the limit of a large number of steps. Then one can expect to apply the resulting aggregate rule in a large number of ways. And much as we expect the limit of our spatial hypergraphs to be able to be represented—at least in certain cases—as a continuous manifold, we can expect something similar here. In particular, we can think of ourselves as winding up with a very large number of permutations corresponding to equivalent rule applications, which in the limit can potentially correspond to a Lie group.

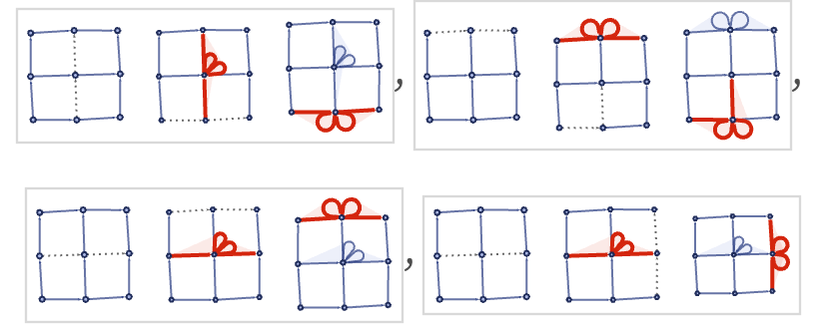
Each different possible choice of how to apply the rule corresponds to a different event that is represented in the multiway graph, and the multiway causal graph:

But the important point is that local choices of how the rule is repeatedly applied must always correspond to purely branchlike connections in the multiway causal graph.

The picture is analogous to the one in traditional mathematical physics. The spatial hypergraph can be thought of as a base space for a fiber bundle, then the different choices of which branchlike paths to follow correspond to different choices of coordinate systems (or gauges) in the fibers of the fiber bundle (cf. [135][136]). The connection between fibers is defined by the foliation that is chosen.

There is an analog when one sets up foliations in the spacetime causal graph—in which case, as we have argued, causal invariance leads to general covariance and general relativity. But here we are dealing with branchlike paths, and instead of getting general relativity, we potentially get gauge theories.

In traditional physics, local gauge invariance already occurs in classical theories (such as electromagnetism), and it is notable that for us it appears to arise from considering multiway systems. Yet although multiway systems appear to be deeply connected to quantum mechanics, the aggregate symmetry phenomenon that leads to gauge theories in effect makes slightly different use of the structure of the multiway causal graph.

But much as in other cases, we can think about geodesics—now in the multiway causal graph—and can study the properties of the effective space that emerges, with local phenomena (including things like commutators) potentially reflecting features of the Lie algebra.

In traditional physics an important consequence of local gauge invariance is its implication of the existence of fields, and gauge bosons such as the photon and gluon. In our models the mathematical derivations that lead to this implication should be similar. But by looking at the evolution of our models, it is possible to get a more explicit sense of how this works.

Consider a particular sequence of updates with the rule shown above:

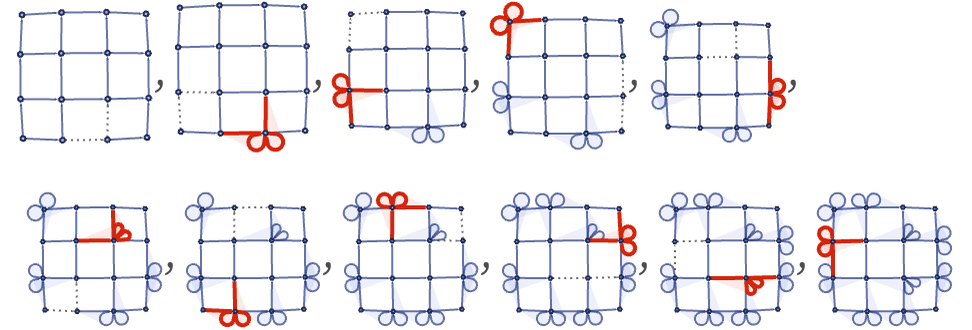
At the beginning, symmetry effectively allows many equivalent updates to be made. But once a particular update has been made, this has consequences for which of the possible updates—each independently equivalent on their own—can be made subsequently. These “consequences” are captured in the causal relationships encoded in the multiway causal graph—which have not only branchlike but also spacelike extent, corresponding in essence to the propagation of effects in what can be described as a gauge field.