download pdf 
ARXIV
peer reviewLike string substitution systems, our models can have the important feature of causal invariance [1:9.9]. In analogy with neighbor-independent string substitution systems, causal invariance is guaranteed if there is just a single relation on the left-hand side of a rule.
Consider for example the rule:
Starting from a single self-loop, this gives the multiway system:
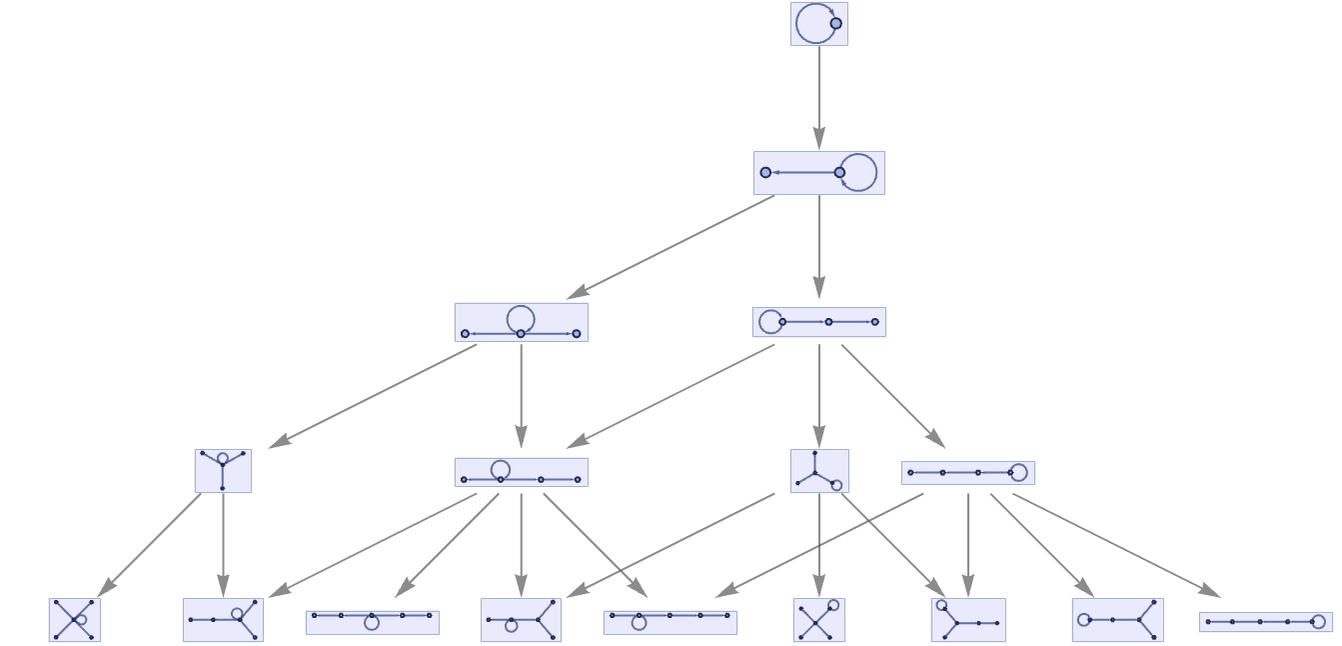
As implied by causal invariance, every pair of paths that diverge must reconverge. And looking at a few more steps, we can see that in fact with this particular rule, branches always recombine after just one step:
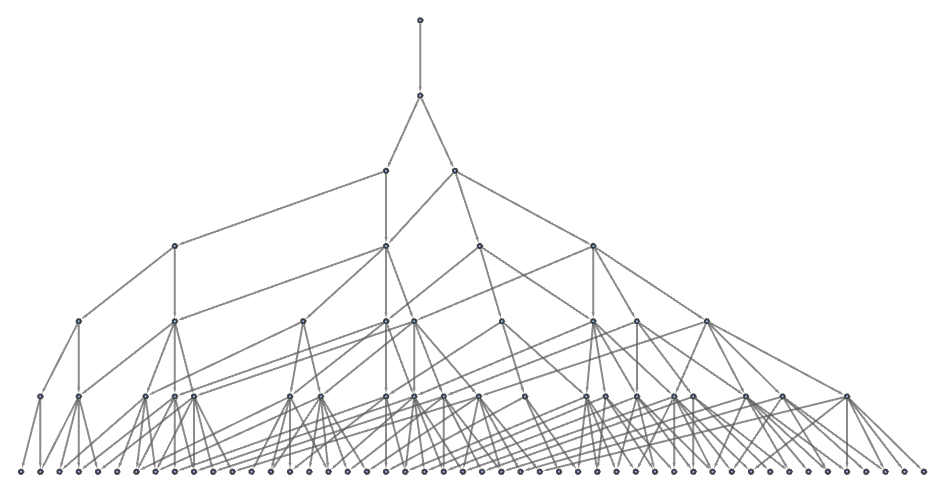
The different paths here lead to hypergraphs that look fairly different. But causal invariance implies that every time there is divergence, there must always eventually be reconvergence.
And for some rules, different paths give hypergraphs that do look very similar. An example is the rule
where the hypergraphs produced on different paths differ only by the directions of their hyperedges:
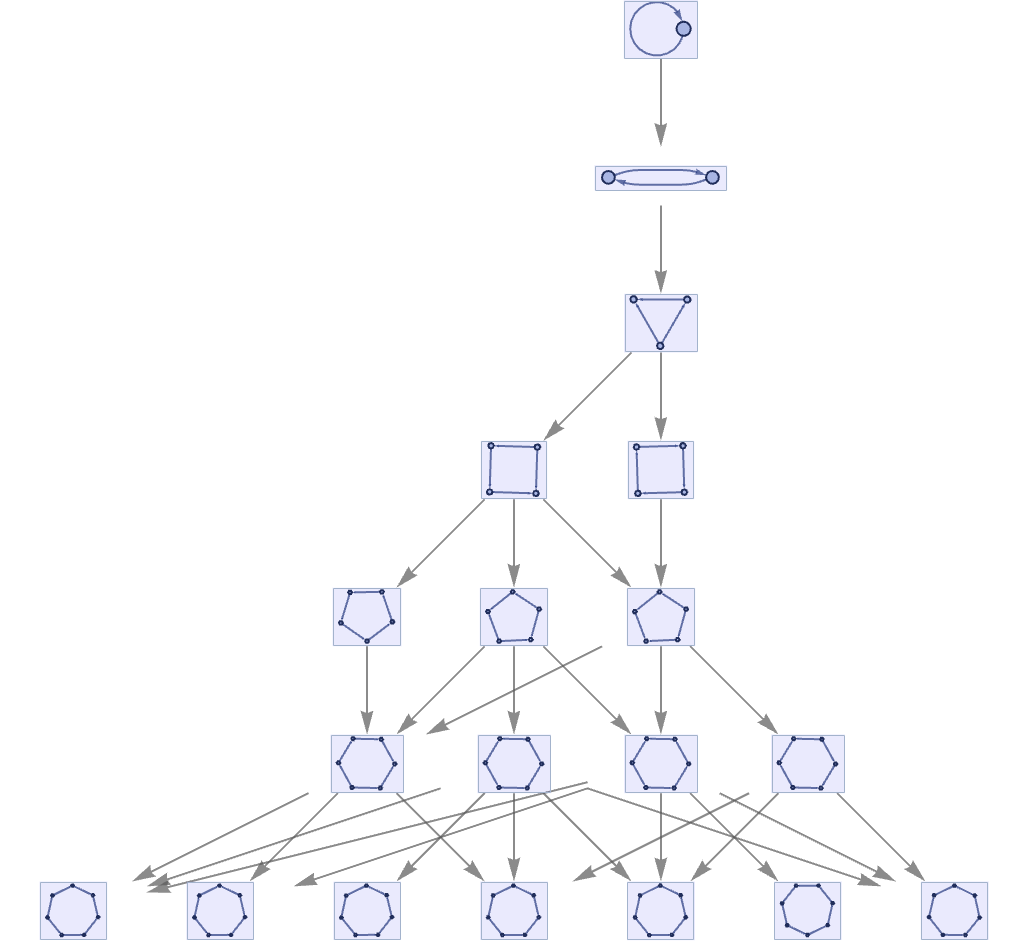
For rules that depend on more than one relation, causal invariance is not guaranteed, and in fact is fairly rare. Of the 4702 inequivalent 22 32 rules, perhaps 5% are causal invariant.
In some cases, the causal invariance is rather trivial. For example, the rule
leads to a multiway graph that only allows one path of evolution:
A less trivial example is the rule
which yields the multiway system:
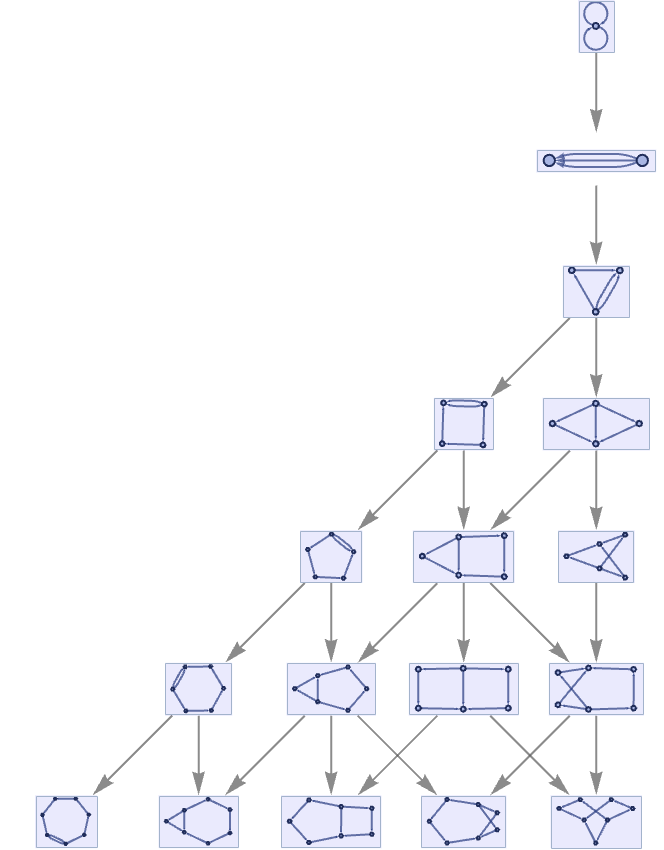
With our standard updating order, this rule eventually produces forms like
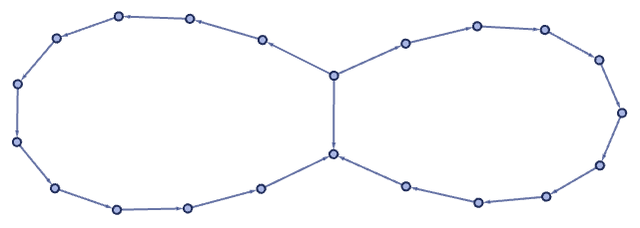
but the multiway system shows that other structures are also possible.
As another example, consider the rule
which with our standard updating order gives:
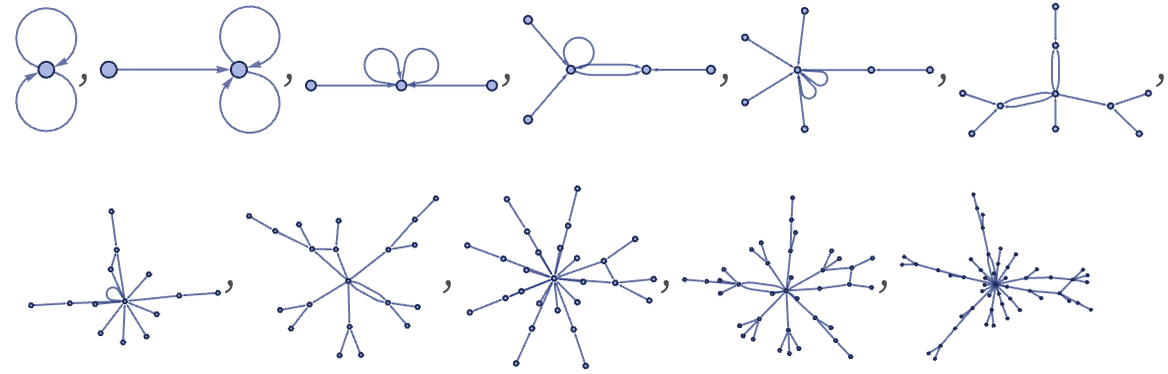
The multiway system for this rule branches rapidly
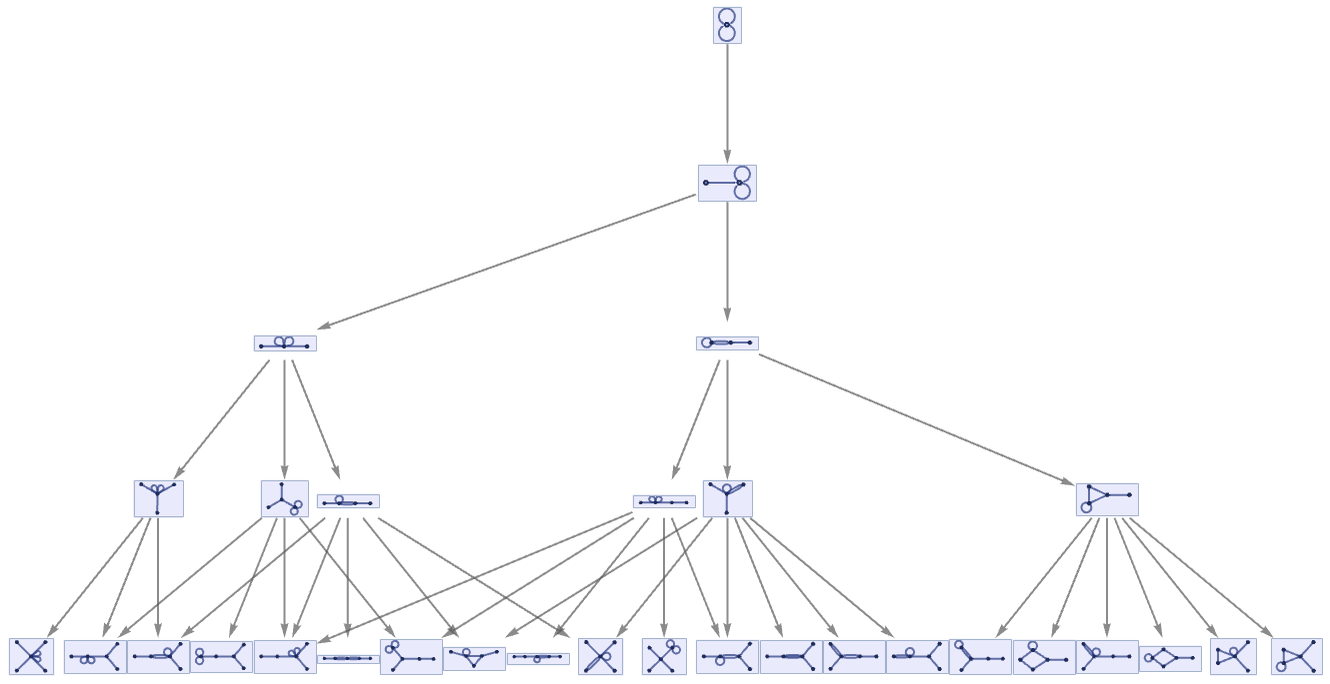
but every pair of branches still reconverges in one step.
provides an example of causal invariance in which branches can take 3 steps to converge:
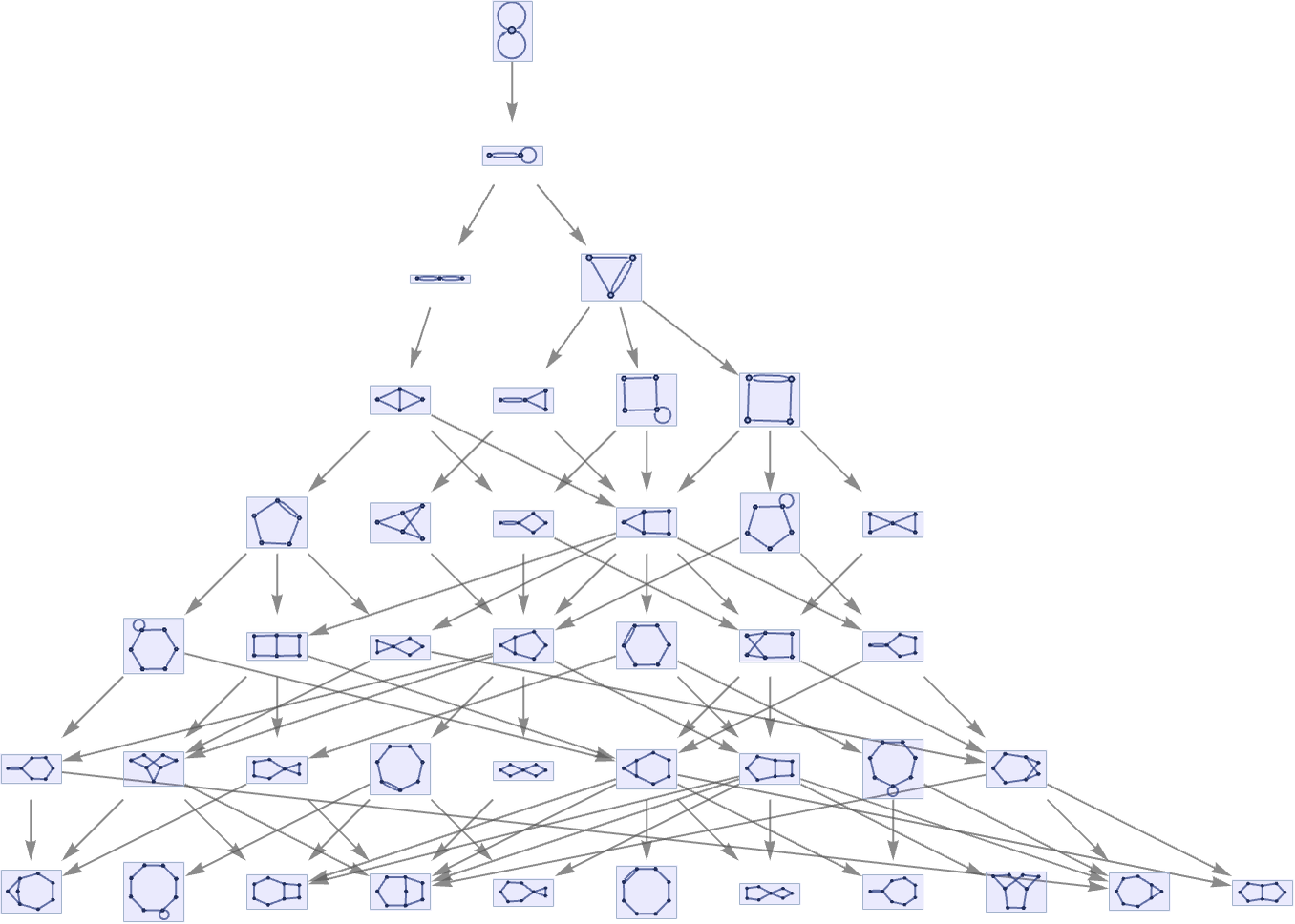
Among all possible rules, causal invariance is much more common for rules that generate disconnected hypergraphs. It is also perhaps slightly less common for rules with ternary relations instead of binary ones.