3.3 Initial Conditions

In addition to enumerating rules, we can also consider enumerating possible initial conditions. Like each side of a rule, these can be characterized by sequences n₁^k₁n₂^k₂... which give the number of relations n_i of arity k_i.

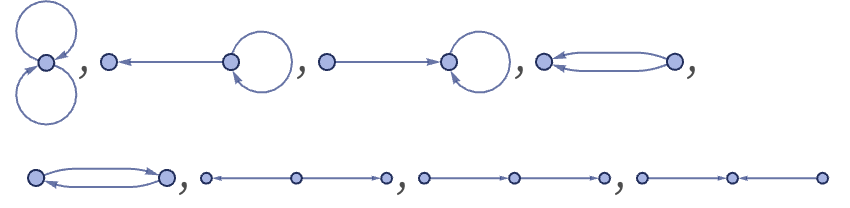
The only possible inequivalent 1₂ initial conditions are {{1,1}}, corresponding a graph consisting of a single self-loop, and {{1,2}}, consisting of a single edge. The possible inequivalent connected 2₂ initial conditions are:

These correspond to the graphs:

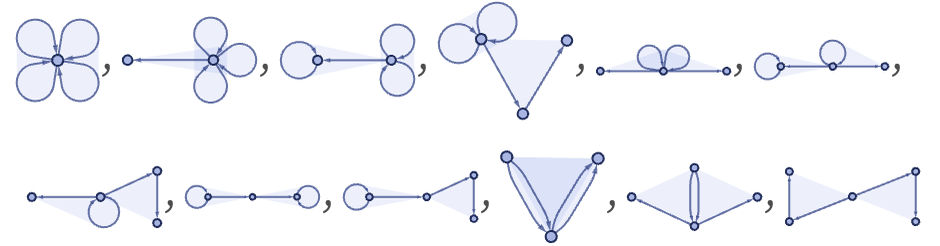
The possible inequivalent 1₃ initial conditions are:

These correspond to the hypergraphs:

There are 102 inequivalent connected 2₃ initial conditions. Ignoring ordering of relations, these correspond to hypergraphs with the following structures:

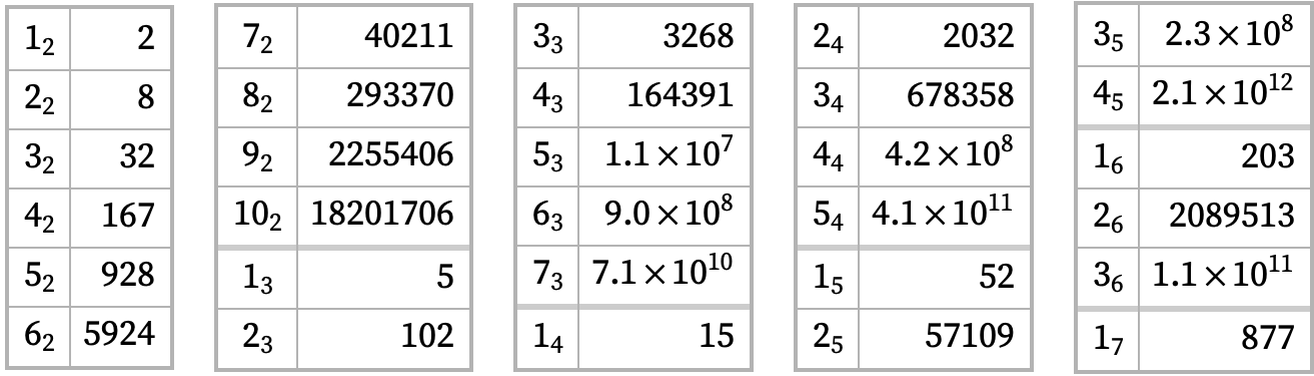
Ignoring connectivity, the number of possible inequivalent n₁ initial conditions is PartitionsP[n], the number of 1_n ones is BellB[n], while the number of n₂ ones can be derived using cycle index polynomials (see also [11:A137975]). The number of inequivalent connected initial conditions for various small signatures is as follows (with essentially the same Bell number estimates applying as for rules) [12]:

A rule can only apply to a given initial condition if the initial condition contains at least enough relations to match all elements of the left-hand side of the rule. In other words, for a rule with signature n_k  … there must be at least n k-ary relations in the initial condition.

One way to guarantee that a rule will be able to apply to an initial condition is to make the initial condition in effect be a copy of the left-hand side of the rule, for example giving an initial condition {{1,2},{1,3}} for a rule with left-hand side {{x,y},{x,z}}. But the initial condition that in effect has the most chance to match is what is in many ways the simplest possible initial condition: the “self-loop” one where all elements are identical, or in this case {{0,0},{0,0}}. In what follows we will usually use such self-loop initial conditions Table[0,n,k].