5.13 Limits of Causal Graphs

Much as we did for hypergraphs in section 4, we can consider the limiting structures of causal graphs after a large number of steps. And much as for hypergraphs, we can potentially describe these limiting structures in terms of emergent geometry. But one difference from what we did for hypergraphs is that for causal graphs, it is essential to take account of the directedness of their edges. It is still perfectly possible to have a limit that is like a manifold, but now to measure its properties we must generate the analog of cones, rather than balls.

Consider for example the simple directed grid graph:

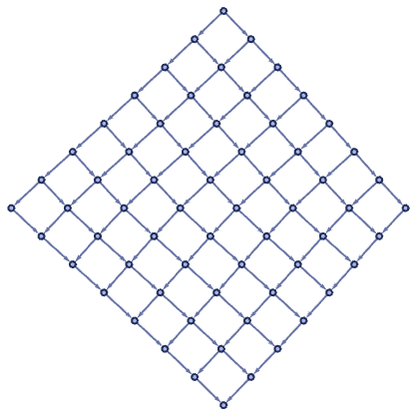
Now consider starting from a particular node, and constructing progressively larger “cones”:

We can call the number of nodes in this cone after t steps C_t. In this case the result (for t below the diameter of the graph) is:

And in the limit of large graphs, we will have:

We can also set up a 3D directed grid graph

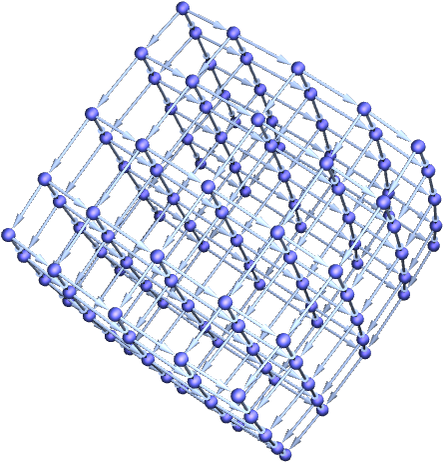
and generate a similar cone

for which now C_t~ t³.

In general, we can think about the limits of these grid graphs as generating a d-dimensional “directed space”. There is also nothing to prevent having cyclic versions, such as

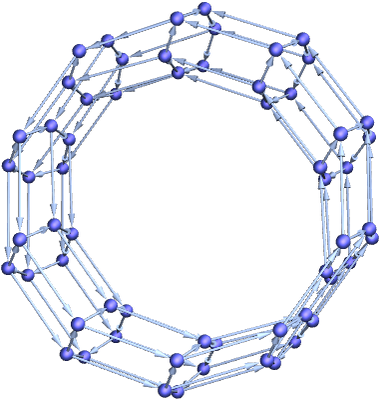
and in general a family of graphs that are going to behave like d-dimensional directed space in the limit will have C_t~ t^d.

In direct analogy to what we did with hypergraphs in section 4, we can compute C_t for causal graphs, and then estimate effective dimension by looking at its growth rate. (There are some additional subtleties, though, because whereas at any given step in the evolution of the system, V_r can be computed for any r for any point in a hypergraph, C_t can be computed only until t “reaches the edge of the causal graph” from that starting point—and later we will see that the cutoff can also depend on the foliation one uses.)

Consider the substitution system:

This generates the causal graph:

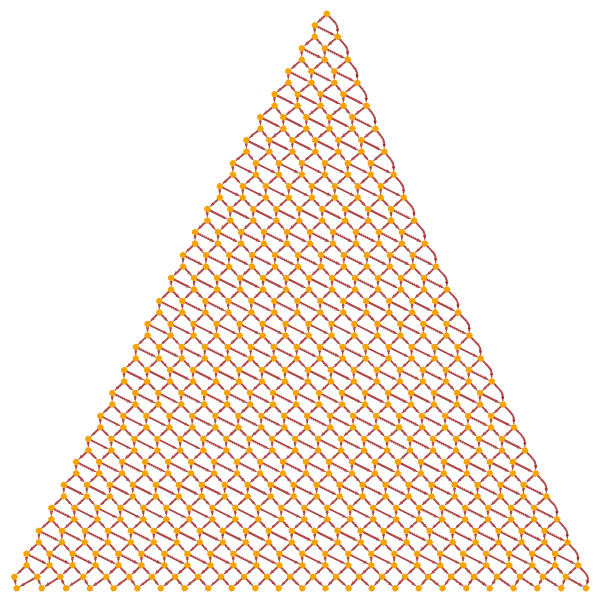
The log differences of C_t averaged over all points for causal graphs obtained from 10 through 100 steps of evolution have the form (the larger error bars for larger t in each case are the result of fewer starting points being able to contribute):

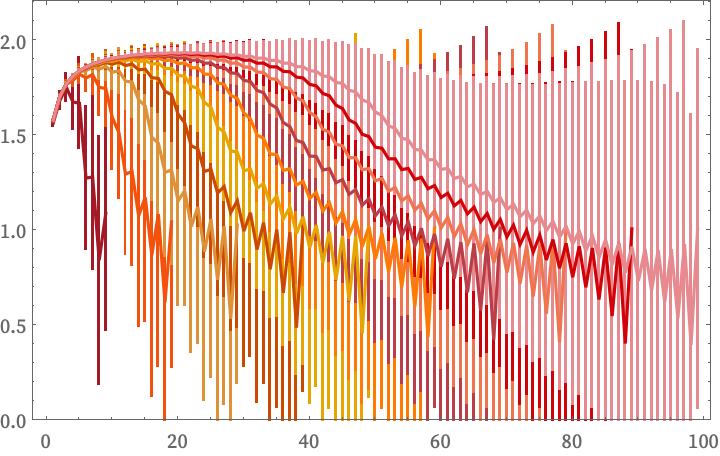
As expected, for t small compared to the number of steps, the limiting estimated dimension is 2.

Most of the other causal graphs shown in the previous subsection do not have finite dimension, however. For example, for the rule AA  AAA the causal graph has the form

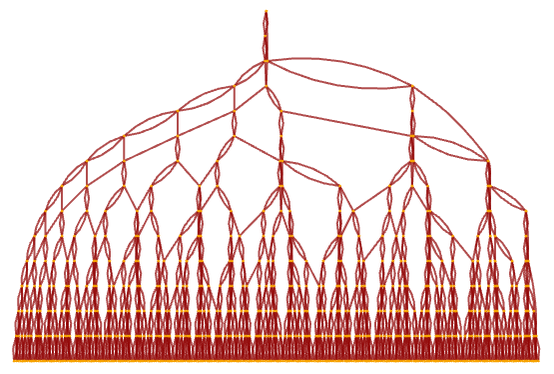
which increases exponentially, with .

The limits of the grid graphs we showed above essentially correspond to flat d-dimensional directed space. But we can also consider d-dimensional directed space with curvature. Although we cannot construct a complete sphere graph that is consistently directed, we can construct a partial sphere graph:

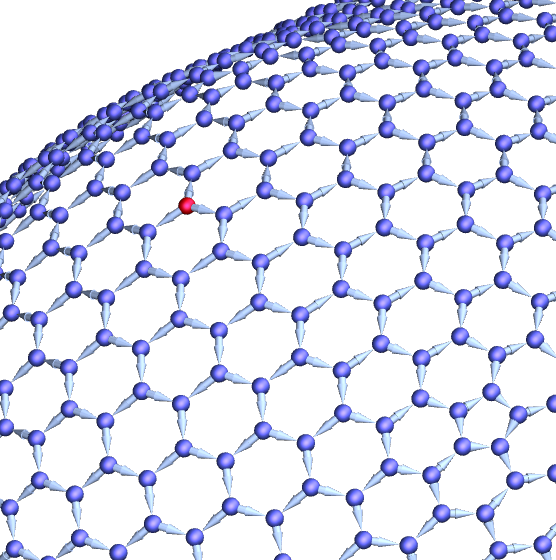
In a layered rendering, this is:

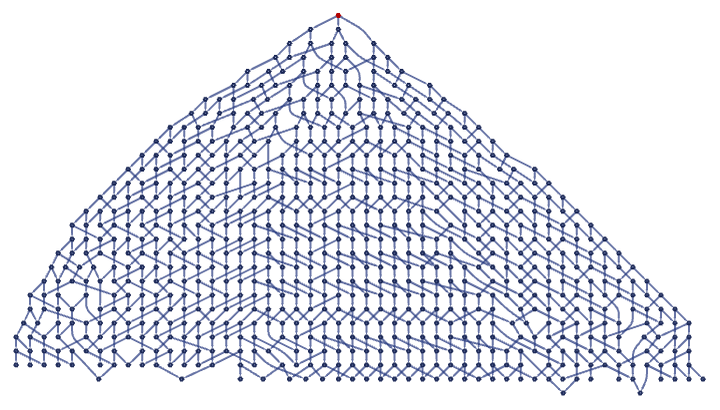
Once again, we can compute the log differences of C_t (the similarity of sphere graphs means that using larger versions does not change the result):

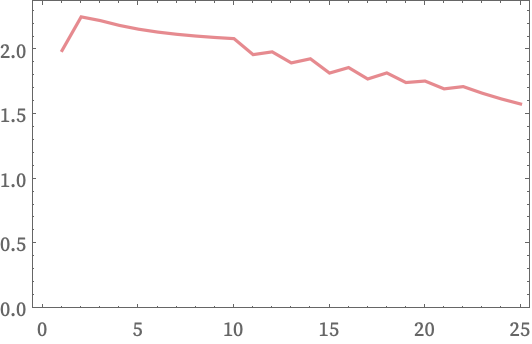
The systematic deviation from the d = 2 result is—like in the hypergraph case—a reflection of curvature.